5章．区間推定の説明

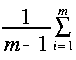ある観測対象全体の集合を母集団と呼び、その母集団の中からいくつか選んで観測した対象を標本と呼ぶ。

母集団のばらつきの度合いを示すものを母分散(σ²)という。母分散の推定値は次式で示されるような不偏分散(V=ν²)が正しい推定値になり得るとされている。ただし、母集団の個数nは標本の個数mに比べて極めて大きく無限に近いものと仮定する。
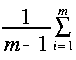不偏分散(ν²)=偏差平方和÷自由度=偏差( $x_{i}-upperbar x$ )の平方和÷(標本の大きさ(m)-1)= $frac{1}{m-1}sum{i=1}{m}$ ( $x_{i}-upperbar x$ )²

標本の大きさがmなのに不偏分散の自由度がm-1であるのは、不偏分散を求める式の中のm個の観測値(x_i)がお互いに完全には独立ではなく、どれか一つの観測値は他のm-1個の独立な観測値と標本平均から求められるからである。

大きさnの正規母集団N(μ,σ²)から大きさmの標本を取り出したときの標本平均は正規分布になる。この正規分布の分散はもとの正規母集団N(μ,σ²)の母分散(σ²)の1/mになることが知られている。すなわち、標本平均の期待値、分散、標準偏差はそれぞれ

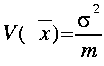
$V (upperbar x) = {frac{sigma^2}{m}}$
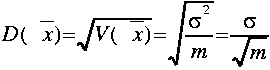
$D (upperbar x) = sqrt{V (upperbar x)} = sqrt{ frac{sigma^2}{m}} = frac{sigma}{sqrt{m}}$
となる。

区間推定においては、母分散の値が不明な時、標本平均の標準化の式の中の母分散を不偏分散で置き換えて得られる統計量がn-1のt分布に従うことを利用して、次の式によって信頼区間を求めることになる。
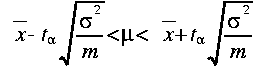
$upperbar x - t_{alpha} sqrt{ frac{sigma^2}{m}} lt mu lt upperbar x + t_{alpha} sqrt{ frac{sigma^2}{m}}$
なお上式において $t_{alpha}$ は、自由度n-1のt分布における上側確率α/2の臨界値である。