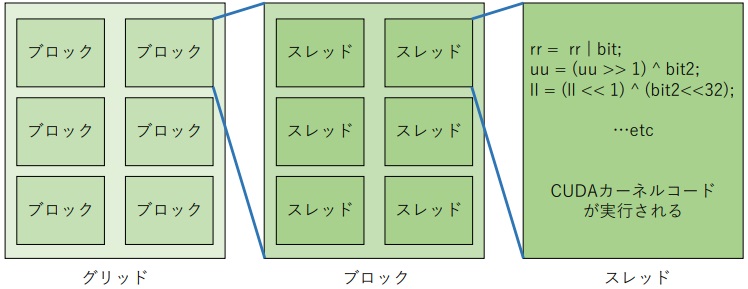
- 図1：CUDAの階層構造
GPGPUの性能向上は著しい．その為，複数の性能の異なるGPGPUノードを所持することはしばしば有り得る． 本研究ではMapReduce型の計算問題に対して，複数の性能の異なるGPGPUノードを並列に使用し，高速に解く手法を提案する． これは実測値に基づく整数計画問題によるジョブ割当を行うものである． したがって，異機種の性能差だけではなく，ネットワーク特性なども吸収して実行時間を最適化する．
数値計算，科学技術演算，ビッグデータ解析，機械学習などの領域で，GPGPU (General-Purpose computing on Graphics Processing Units，GPUを用いた汎用計算) によるソフトウェア処理の高速化が図られてきた． 並列計算をGPGPUで高速に行うべく，グラフィックボード (GPUを搭載した演算ボード) を搭載するパソコンを購入するケースは増えつつある．
一方，現在のGPUは開発スパンの短期化と性能向上が著しい． NVIDIA社は1〜2年程度で新型GPUを発表している． 最新GPUは1世代前の2倍の実効性能が出る場合さえある． 利用者の立場からは，予算に見合った高性能なGPGPU計算ノードが常に必要である． したがって，最新型として入手したGPGPU計算ノードが数年で陳腐化することは否めない． 常に高性能なGPGPU計算ノードを入手し続けると，陳腐化した比較的高性能なGPGPU計算ノードも多く所有することになる．
また，スーパーコンピュータなどの複数ノード動作が前提の場合，殆どが統一されたハードウェア構成である． 更に，今日におけるスーパーコンピュータのノード間通信環境は，数十Gbpsの通信（InfiniBandや光伝送装置）が用いられつつある． これにより，ハードウェア起因のパフォーマンスロスは低く抑えられ，複数ノードによる分散コンピューティングは比較的容易に行える ．一方で異世代・異機種のハードウェアでの不均一環境下では，性能差の考慮などから積極的に行われてこなかった．
本研究では，並列計算問題としてMapReduce計算に注目し，これを複数のヘテロジニアスなGPGPU計算ノードで計算することを考えた． 並列計算では様々な要因が計算速度に影響を与える為，一概には結論が出せない． 特にノード間通信速度は考慮すべき問題であり，ネットワーク機器なども計算速度に影響を与えるものと考えられる． 本実験においては1Gbps Ethernetを用いた． しかしながら，MapReduce計算はノード間通信が比較的少ない為，ネットワーク性能が計算速度に大きく影響しないと思われる． 更に複数ノード間の計算割当が容易であると考えられる． この点から，複数ノード間でのMapReduceの協調計算手法を提案し，評価を行った．
本論文の構成は以下の通りである． 1章では本研究の動機と目的を述べる． 2章では本論文で用いる用語や技術についての説明を述べる． 3章では本研究に関連する研究について述べる． 4章では本研究の提案手法について述べる． 5章では提案手法を基にした実験と結果の評価を述べる． 6章では本論文全体のまとめを述べる． 以後は，参考文献，付録にプログラムを載せる．
CUDA(Compute Unified Device Architecture)とは，NVIDIA社によって開発された，GPU上で動作する汎用並列計算プラットフォーム及びプログラミングモデルである[1]． C，C++，Fortran，，Python，MATLABなどのプログラミング言語の内部に，その言語の拡張仕様として__global__や__device__接頭語を付与したCUDAカーネルコードを埋め込む事で，該当の並列計算部分をGPUへオフロードする事ができる． CUDAはCPU及びメインメモリはホスト，GPUはデバイスと呼ぶ概念で互いに接続をする． GPUへのオフロードは，ホストメモリで生成したデータをGPUへ明示的にコピーし，GPUで計算し，計算結果をGPUからホストメモリへコピーするという一連のプロセスが基本である． CUDAはグリッド，ブロック，スレッドという階層構造での並列化を行う． 階層構造を図1に示す．
GPUの機種によって数値は異なるが，例としてGeForce GTX1080Tiでは，グリッド数最大65535×65535×1，ブロック数最大1024×1024×64，1ブロックあたり最大1024個のスレッドを同時に扱う事ができる． 結果として65535×65535×1024個のスレッドを同時起動して並列計算をする事ができる． この数はGPUに搭載されるCUDAコア数 (GTX1080Tiでは3584コア) を大幅に超えているが，これはCUDAアーキテクチャが処理時間の隠蔽を繰り返す設計思想に基づくためである． 簡単な例を挙げると，メモリアクセスをするスレッドと計算をするスレッドが同時に実行されれば，それぞれの時間を互いに隠蔽し合う事となる． これを多数のスレッドで実行する事で，処理時間の隠蔽が重なり，結果としてGPUは最大限の計算能力を発揮する事ができる．
CUDAカーネルコードはプログラミング言語の拡張として演算を記述する事ができる． 従ってエンジニアや研究者は取り扱う問題のアルゴリズムなど，本質の部分に集中して実装する事ができる． GPGPU用の特別な処理は，メモリコピーとカーネルの実行など，最小限の手間で済む．
MPI(Message Passing Interface)とは，並列コンピューティングのデファクトスタンダードとも言える規格である． MPIはTCPを採用した通信プロトコルである． プログラムのソースコード内に，MPIによる通信を行うMPI_Send関数やMPI_Recive関数などを記述する事で，データ通信を行う． 通信はメッセージと呼ばれる単位で行われ，情報をバイト列にして送受信を行う． MPIはEthernetやInfinibandの他，内部バス接続のデュアルCPU間の通信もサポートする． また，同一CPU上でスレッドを複数起動させる事で，同一CPU上でアプリケーションの並列実行をする事もできる．
主要なMPIパッケージは，OpenMPI，MPICH，MVAPICH，Intel MPIなどが知られている． 多くのMPIパッケージにて直接動作するプログラミング言語は，C，C++及びFortranである． MPIパッケージは並列動作させたいノード全てで統一する必要がある． 本研究では各ノードでCUDAを使用する為，CUDA-Awareに対応したOpenMPIを用いる． CUDA-Aware MPIは，GPUの共有メモリに対して直接データ送受信が可能である．
ヘテロジニアスコンピューティング(Heterogeneous computing)とは，異種混合プロセッサ上で演算を行わせて目的を達成する計算モデルである． 用途に応じて適切なプロセッサを選択する事で，プログラム全体の処理効率を高める事ができる．
スーパーコンピュータなど，同機種のCPUを多数搭載した際の分散コンピューティングは古くから達成され，成熟された技術と言えるだろう． だが異機種・異仕様のハードウェアを組み合わせた場合は，スケジューリング技術が単純な分散ではなくなってしまう他，実行される命令や，処理動作の仕様が異なる． 従ってヘテロジニアス環境に対応する為には，一般的に高い技術力が求められる． なお，この課題に対しCUDAでは，ヘテロジニアス環境となるCPUとGPUの動作の差をプログラミング言語の拡張となる形で吸収しており，開発を行い易くする為の環境が整えられている．
本研究においては，世代及びCUDAコア数や動作クロックなどの仕様が異なる異機種GPUに加え，ホストの異機種CPUも含めたヘテロジニアスコンピューティングネットワークを形成する．
MapReduce は，入力列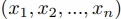
に対して，関数
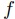による
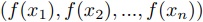を計算するMap操作と，結合法則を満たす二項演算
による
を計算するReduce操作を総称したものである．
計算コア数がk個である時，Map操作は各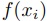
を並列計算できる．
したがって，並列計算の段数は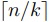
となる．
一方Reduce操作の一回目は，奇数番と偶数番同士で結合させることで，
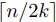⌉段の並列計算となる．
その後，隣接項を相互に結合させることで，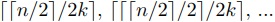
段の並列計算が生じる．
従って総段数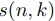
は(1)のように見積もれる．
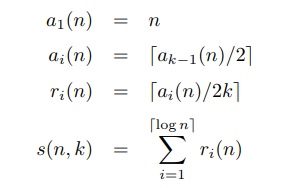(1)これは以下のように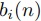
を定義すると，
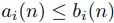となり，(2) のように概算できる．
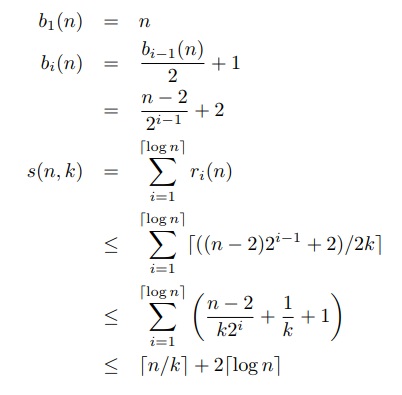(2)整数計画問題とは，目的関数が線型関数であり，なおかつ各変数を整数に限定した線型関数の等式と不等式で制約条件が記述できる問題である． 整数計画問題が適用される事例は，業務におけるタイムスケジューリングや巡回セールス問題などが挙げられる． 整数計画問題は一般にNP困難問題である． しかしながら，ソルバの開発や計算機の高性能化に伴い，実用的には十分短時間で解を導き出す事ができる問題サイズも存在する． 本研究では，C言語で記述できるGLPKソルバ[11]を採用し，実用的な時間で問題セグメントの割り当てを行う．
NQueens問題とは，N×Nのチェス盤上で，チェスのクイーンが互いに取り合わない置き方の総数を求めるパズルである． チェス盤におけるマスはN2個あり，そこにN個のクイーンが配置される． 配置可能なパターンが増える事で，組み合わせ爆発が発生する． 特定の盤面において，互いに取り合うか否かは盤面の面積に比例する程度の計算時間でチェックできる． その為，虱潰し法でNQueensを求める問題はMapReduceにより計算できる． なお，NQueens問題に対する虱潰し法よりも本質的に効率の良い数え上げ手法は未発見である． 本研究ではMapReduce計算のベンチマークテストとして，このNQueens問題を使用する．
Zhangらは，データセンタのヘテロジニアスマルチコア環境におけるHadoop計算の性能低下原因を解析し，性能向上の為のタスク割り当て機構の提案を行った[2]． この研究では，ヘテロジニアス環境におけるMapReduceの性能低下は，性能差を考慮しない不適切なタスク割り当てが原因であることが示された． タスクを適切に割り当てる為，Map処理とReduce処理でそれぞれ異なるアルゴリズムを持たせ，ラグランジュの未定乗数法を用いた最適化により各ノードへタスクを割り当てることを提案した． この結果，ヘテロジニアスクラスタ上での標準実装のHadoop計算と比較し，30%から70%の速度向上を達成している． 高橋らは，CPUを用いたCFD(計算流体力学)，FEM(有限要素法)，FFT(高速フーリエ変換)，及びHPL(高性能Linpack)の4種類の並列アプリケーションについて，各実装アルゴリズムを基に，計算量から実行時間予測のモデルを立てて分散をさせる研究を行った[3]． また，Cuencaらは，CPUの不均一クラスタにおける同種の並列計算において，問題の分散に対する計画の立て方を2個示した[4]． 1つは問題をハードウェア構成に沿った分割をし，その問題専用に特定のアルゴリズムを組む方法である． これは実現できた際の実行効率は高くなるが，古典的なアルゴリズムに分散アルゴリズムを組み込むという静的な手法である為，プログラミングコストが高く，更にハードウェア変更時には対応が必要となる． もう1つは動的に分散させる為のプログラムを追加し，MPI通信によりリアルタイムにジョブ分散を行わせる方法である． システムの処理速度や通信時間などの特性パラメータを並列処理中に測定し，パラメータを用いて処理時間を理論的に導いた上で処理を自動的に分散させる． しかしながら，不均一なハードウェア環境や負荷が計算内容によって変化する場合，プロセッサの割り当て問題はNP完全問題であり，自動的な最適プロセッサの選択は達成が難しい点を挙げている．
吉瀬らは2004年，68台のIntel XeonノードによりN=24の時のNQueens問題を22日で解いた[5]． Preußerは2016年，求解用にFPGAクラスタを作成し，1年以上の計算により，NQueens問題をN=27まで計算した[6]． 彼らはNQueens問題がベンチマークテストに優れていることも言及している． GPUを用いたNQueens問題の高速化では，文献[7][8][9][10]にて，実装最適化や探索量の削減が議論及び実験されてきた． 一方でこれらの研究では，マルチノード化や，1ノードに複数台のGPUを搭載したマルチGPU対応は検討されていない． 本研究では荻野谷らの実験[10]を参考に，異種混合GPGPU上のMapReduce問題として，NQueens問題を評価指標とした．
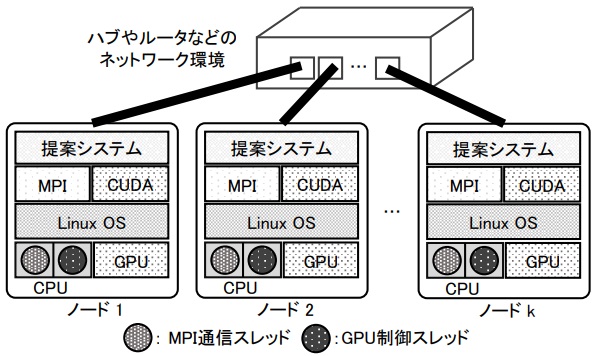
ノードの構成に必要なハードウェア及びソフトウェア条件を示す． また，本提案手法におけるノード構成図を図2に示す．
各ノードには，1個以上のCUDAが動作するNVIDIA GPUが必要である．
各ノードでは，CPUによるMapReduceの準備や通信を行うMPIスレッドと，GPUでMapReduceの並列計算部を行う為のGPU制御スレッドの2つがペアとなる． GPU1個あたり計2スレッド，つまりCPUコアを2コアずつ使用する．
Ubuntu，CentOS，OpenSUSEなど，CUDAが動作するLinux 64bit OSを用いる．
NVIDIA社の公式ページからパッケージのダウンロード及びインストールが必要である
2章で述べたように，MPIには幾つかのパッケージがあるが，MPI+CUDAを有効に活用する為にはCUDA-Awareに対応したMPIの選択とインストールが必要である[12]． 該当するパッケージはOpenMPIやMVAPICH2などである．
本実験においては，各ノードはEthernetでL3スイッチへ接続することとした． MPIプロセスは内部処理でIPアドレスを指定して動作する為，各ノードのIPアドレスの割り当ては静的設定する必要がある．
MapReduce計算をヘテロジニアス並列計算にて行う手法を述べる． 基本的なアイディアは，次の通りである．
各計算ノードに対して幾つかの問題を複数個渡し，実行速度を測定して，問題数と実行時間の関係を求める．
残った問題数を解くのに最適な割当を，各ノードのサンプル実行速度を基に整数計画問題としてソルバに解かせる．
求めた分割数にしたがって，残りの問題を並列に解く．
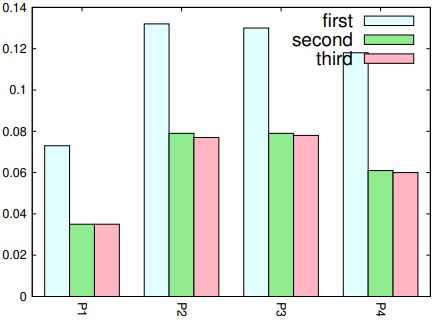
しかし，同じ問題を解く実行速度を複数回測定すると，初回の実行速度のみ遅くなる事が判明した．(図3)． この為，初回の計測結果は計算速度の推定に使わず，2回目以降を使うようにする．
関数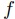と二項演算により，入力値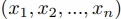に対して，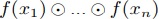
の値を求める．
ここでm個の計算ノード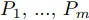
を用いるとする．
また，入力セグメントを考える．
を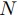
分割することを考える（がで割り切れない場合は，ダミーの入力を与えることもある）
ここで，セグメント番号
から
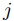まで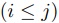
の入力部分列を
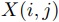で表すとする．
入力部分列を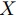
と表すこともあるが，この時入力部分列のセグメントサイズを
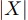で表す．
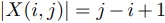である．
また，各計算ノードでは予めMapReduce計算が可能であるとして，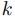
番目のノードにおける入力部分列Xを計算して求めた値を
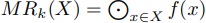で表す．
更にそれに要した時間を計測できるとして，
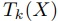で表す．
提案手法は，この各計算時間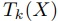が入力値によらず，入力列の数に対して
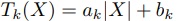であると仮定した手法である．
以下，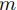
はあまり大きい数ではなく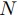，は3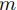より十分大きいとする．
またサンプリングサイズを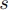
とする．
はじめに，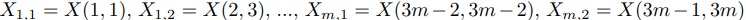
と置く．
.jpg)
とする．ここで，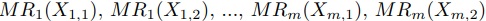
を計算した後，各
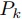で
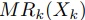を並列計算することを考える．
並列計算の時の最大実行時間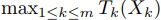
を最小にするような入力列の分割を求めたい．
仮定より，以下を満たす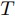
を最小化する整数
を既存の整数計画問題を解くソルバで求める．
なお実験においては，整数計画法を解くためにGLPK[11]を用いた．
このようにして求めた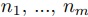に対して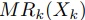を並列計算する．
最終的に，解として(3)を出力する．
この擬似プログラムを図4，図5に示す．
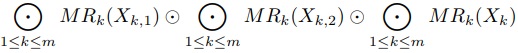(3)
#define M ノード数
time_t s[M][3],t[M][3];
char* X;
int phase=0;
long measure(int block){
long rans,answer=0;
int i,j;
for(i=0; i<M; i++){
s[i][phase]= 時刻;
MPI_send( ノード i に X の中から問題を block 個);
}
for(i=0; i<M; i++){
MPI_receive( ノード j から解の個数 rans を受信);
t[j][phase]= 時刻;
answer += rans;
}
phase++;
return answer;
}
long solve(int* n){
long rans,answer=0;
int i,j;
for(i=0; i<M; i++){
MPI_send( ノード i に X の中から問題を n[i] 個);
}
for(i=0; <M; i++){
MPI_receive( ノード j から解の個数 rans を受信);
answer += rans;
}
return answer;
}
int main(void){
int answer=0;
int n[M];
X= 問題集合;
/* phase0 */
answer += measure(1);
/* phase1 */
answer += measure(1);
answer += measure(2);
/* phase2 */
n=IPsolver(X,s,t より残りの問題の最適分割を求める );
/* phase3 */
answer += solve(n);
printf("%g\n",answer);
return 0;
}
図4：Master CPU側疑似コード
#define N 19
___global___ void nqueen(char* board, int* answer){
char myboard[N];
long myanswer=0;
int index = 自分のコアの位置;
myboard 計算(board,index);
for(myboard の全ての自由変数を数え上げ){
if( 互いに取り合わない配置 (myboard)) myanswer++;
}
answer[index]=myanswer;
}
int main(void){
char questions[N*N];
long answer;
while(1){
answer=0;
MPI_Receive(questions);
for(questions 中の各 question について){
question から cudaArg1, cudaArg2 作成;
nqueen<<<cudasize/blocksize,blocksize>>>
(cudaArg1,cudaArg2);
answer += cudaArg2 より結果集計；
}
MPI_send( 自アドレスと answer);
}
return 0;
}
図5：Slave側疑似コード
ここで，NQueens問題をMapReduce型の並列計算として解くための実装を述べる． 実装したプログラムは付録にて示す．
GPU数の数十倍以上の問題セグメント数を分割して割り振ると，各問題セグメントの並列計算時間の誤差が数%になることを期待する．
N×Nの盤面のうち，まずCPU側で2×Nを解き，1行目から2行目までのクイーン配置パターンを決定し，問題セグメントとして生成する．
各問題セグメントがMap処理における入力列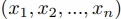に対応する．
問題セグメント数は，N×Nの盤面においてはN2からクイーンが配置不可能なパターンを引いた数となる．
本実験にて用いた19,21,23Queensではそれぞれ，192=361, 212=441, 232=529からクイーンが配置不可能なパターン数を引いた数が問題のセグメント数となる．
各問題セグメントの情報はGPUへ伝送し，残りの(N−2)×NをGPGPUで並列計算し，配置可能な解数をカウントする．
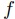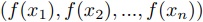この計算はMap処理における関数によるを計算することである．
解き終わった時点での解数の集計結果がNQueens問題の答えとなる．
この集計処理はReduce計算における二項演算によるを計算することである．
問題セグメントのイメージを図6に示す．
異種混合GPU上でのMapReduce計算の評価指標として，NQueens問題の求解時間を測定した．
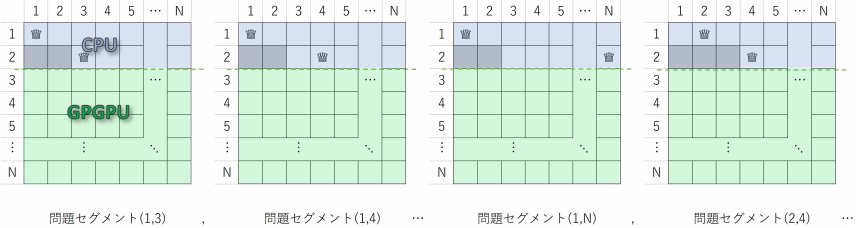
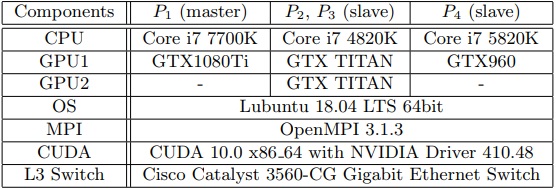
本研究ではノードを3台用意して測定を行った． 但し2台目には2個のGPUが搭載されている為，MPIプロセスとしては2台のノードとして取り扱われる． 表1に各ノードの構成を，図7に各ノードの接続を示す．
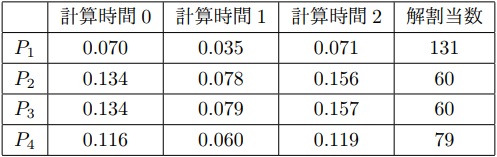
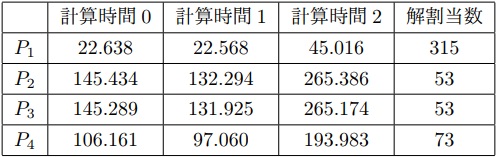
19Queens問題にて，4台のノードに対して問題セグメントを解かせた時間は表2のようになった．
これを元にソルバで残りの解の割当を求めた所，
=(131,60,60,72)となった．
この結果を適用すると，全ての問題を解き終わるまでに要した実測時間は5.28秒であった．
一方，これらのノードで最も高速な
のみで実行すると，求解時間は13.54秒となった．
短縮率は約61%であった．
したがって，単一の高速ノードのみの計算より，実行時間を改善していることが分かる．
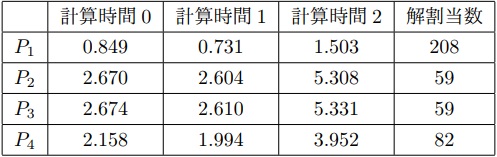
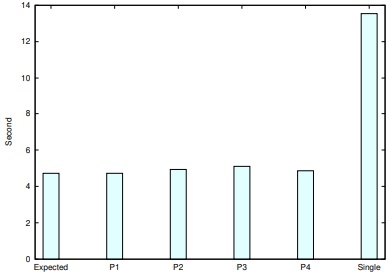
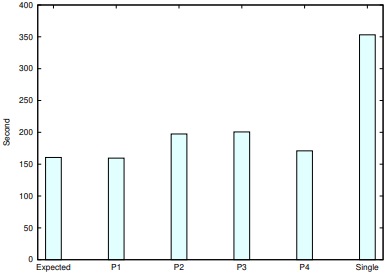
更に21Queens, 23Queensについても同様に実行し，問題セグメントを解かせた時間は表3, 表4である． この結果を適用し，全ての問題を解き終わるまでに要した実測時間は，N=21のとき202.06秒，短縮率は単一ノードの353.18秒に対して約43%であった． N=23のときの実測時間は7626.13秒，短縮率は単一ノードの9852.66秒に対して約23%であった．
実行時間をまとめたグラフを図8，図9，図10に示す．
MapReduce型の問題に対して，問題をセグメント分割し，計算ノードの実行速度を計算し，割当数を求め計算するという手法で，単一な高速ノードのみの計算より実行速度を改善することが示せた． 但し，NQueens問題の各セグメント毎に実測すると，計算時間に差があることが判明した（図11，図12，図13）．
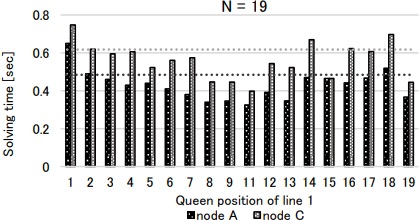
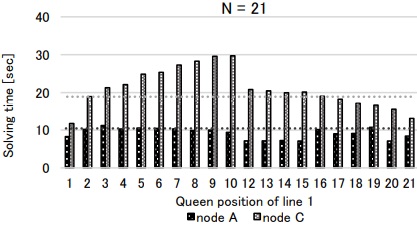
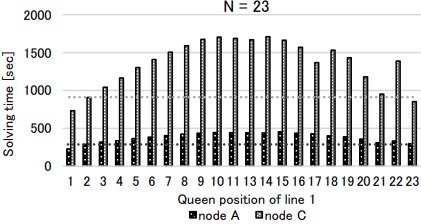
本方式は計算時間の均質さを仮定した手法であるから，計算時間に誤差がある場合の有効性について議論する．
前章では各セグメント毎に均質な計算時間が掛かるとしたが，ここでは最小時間に対して最大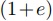
倍の時間が掛かるとする．
計算ノード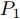の短い方のセグメント数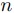に対する計算時間が
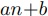であるとする．
計測時に1セグメント，2セグメントを（短, 長）という組み合わせで測定すると，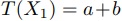
, aplus_b.jpg)
となる測定結果が得られる．
したがって測定値に基づくセグメント計算時間はan-2eaplus_b.jpg)
となり，ほぼ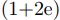
倍長めの予想となる．
一方，計測時に1セグメント，2セグメントを（長, 短）という組み合わせで測定すると，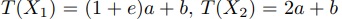
となる測定結果が得られる．
測定値に基づくセグメント計算時間はanplus_2eaplus_b.jpg)
となり，ほぼ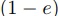
倍短めの予想となる．
ここで，セグメント計算時間が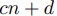
となる計算ノード
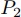と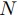個のセグメントを分け合うことを考える．
まず全て均質で測定も正確にできた場合，整数計画法で式(4)を満たす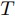を最小化する整数値
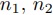を求める．
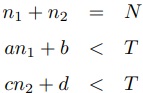(4)これをLP緩和すると，式(5)のように値が求まる．
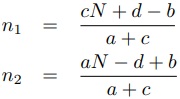(5)一方，計測時に一回だけ測定誤差が出るのみで，後は均質な計算時間となる場合を考える．
その時，（短, 長）となった場合，式6を満たし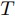を最小化する整数計画法になる．
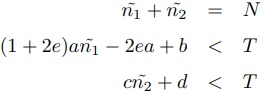(6)これをLP緩和して解くと式(7)が得られる．
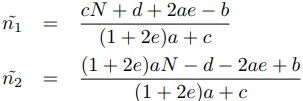(7)この場合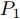，は遅めに見積もられているから，
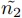が多くなる．
しかし式(8)のように
の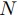の係数は1より小さい．
ゆえに計算時間は倍までは要しないことになる．
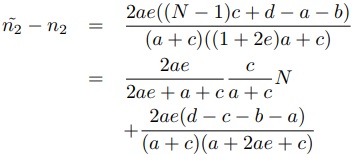(8)これは（長, 短）の場合も同様である． したがって，測定値の誤差が生じても，見積もった計算時間に対して実測が倍以上掛かることはないと言える．
本研究では，異種混合GPUによる不均一なマルチGPGPU環境にて，MapReduce計算を行う手法を提案した． これは，各CUDAノードをMPIで結合し，MapReduceの項目をセグメントに分け，整数計画法で分散させるものである． これにより，単一GPGPU環境よりも計算時間を短縮できることを実験により示した．
MapReduce問題を分割し，線形計画法によりGPUの処理能力に合わせて問題を分配し，ノード全体としてマルチGPUによる高速化を行うアプローチをとった． また，通信のボトルネックを処理中に発生させない為，処理中の伝送が一切不要となる問題の分割を行った．
実験の結果，不均一マルチGPUシステムでも，シングルGPUと比較してMapReduce問題の求解が高速化された． 旧世代GPUもGPGPUアクセラレータとして有用である事が示された．
一方で本提案手法では，問題の分割ができないものや，分割した問題や実データに相互依存性があるものに対しては適用する事ができないか，性能がシングルGPUよりも落ちてしまう． ブロックチェーンのように始点のデータを基に区切り無く生成と計算が続いていくものは，問題を分割する事が出来ないため，本提案手法の適用は不可能である． また，分割したデータに依存性がある場合は，他ノード上のデータ参照の為に通信が必要である． Ethernetの通信速度はGPUの帯域速度と比べて非常に低速である為に，通信待ちが巨大なボトルネックとなりうる．
今後の課題として，MapReduce以外の計算構造をもつ計算やアプリケーションについても，ヘテロジニアス環境に適応した並列計算の実現を試みたい． 更に，問題の処理中に通信が必要な際の通信待ちを極力削減するアルゴリズムや，MPIの代替となる通信パッケージにも取り組みたい．
main関数を含む，NQueens問題を解く為の制御プログラムである．
main関数では，まず全ノードでMPIの初期化と各スレッドのMPIランク情報を収集する． その後は親プロセスとGPUプロセスに分かれる． 親プロセスでは，NQueens問題の盤面データに使う変数の初期化処理の実行と，提案手法にて述べたphase1，phase2，phase3の実行を行う． GPUプロセスでは，後述するsubmit関数から問題セグメントのデータが送られてくるまで待機する． 問題データの受信後はCUDAカーネルコードを起動し，GPGPUによりクイーンの配置を探索する． 全ての問題データを計算し終えたら，マスタープロセスへ解の数を送信する．
これらの関数は，盤面データに用いる変数の初期化及びビット数の決定処理を行う． これにより，後述するnq関数でCPU側でbit演算により盤面データの生成を行うことが可能になる．
nq関数は，盤面における1行目からborderOfCPUandGPU行目（本実験では2行目）までのクイーンの配置パターンをCPUにて決定する関数である． nq関数の引数fromとtoにより，実際にCPU及びGPGPUで計算を行わせる問題セグメントの範囲のみ処理が行われる．
これらの関数は，nq関数で生成されたクイーンの配置パターンを各問題セグメントとして変数に格納し，GPU側へ伝送するものである．
phase1関数では，提案手法で述べたように，各ノードのサンプル時間を測定することが目的である． 問題を1個，1個，2個だけに限定してそれぞれCPUで生成し，各問題をGPGPUで解かせる． GPGPU側ではその処理に要した時間をタイマーで記録する．
phase2関数では，まずphase1にて測定した各ノードのGPGPU処理時間をMPI通信でマスターノードへ集計する． 次に，マスターノードはGLPKソルバにより整数計画法を解き，各ノードへの割り当て数を求める． その後，割り当て数を基に各ノードの担当する範囲を設定する． 最後に，マスターノードは各ノードへ割り当てする問題の範囲をMPI通信で送信する． マスターノードを含む各ノードは割り当て範囲のデータを取得し，phase3にてそれを設定する．
phase3関数では，各ノードはphase2にて得た割り当て範囲に従い，その範囲においてクイーンの配置をGPGPUにて探索する． 探索終了後はマスタープロセスへ解の数を送信し，マスターノードが解の集計を行う．
GPU側でクイーンの配置を探索するCUDAカーネルコードである． このプログラムは，萩野谷らのプログラム[10]を一切改変せず引用し，本実験にて用いたものである． CPUから伝送された各問題セグメントについて，blockIdx.x * blockDim.x + threadIdx.xにてCUDA内で並列化し，各スレッドでビット演算によりクイーンの配置可否を求める． クイーンが配置可能であるときは，解の数をカウントアップする．
MPIに必要なホスト情報を記述したファイルである．
ここでは，本実験で用いた，172.16.1.201をマスターノード (GPU1台) ，172.16.2.202をスレーブノード, 
(GPU2台)，172.16.1.203をスレーブノード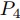
としたhostfileを示す．