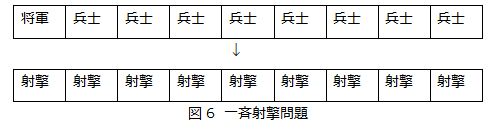
一斉射撃問題とは1957年にJohn Myhillにより提案された問題である。長さ有限の一次元セルラーオートマトンにおいて、一つのセルを将軍、それ以外を兵士とする。将軍が射撃命令を下した時、将軍兵士全員が同時刻で射撃状態へ移行させる問題である。ただし、将軍は1ステップに両隣にしか伝えられず、将軍や兵士は一斉に射撃状態になるまでに、誰一人射撃状態になってはいけないという制約がある。この問題はすでに解かれているが、別のアルゴリズムを考えたり、セルを1次元から二次元や三次元にした問題を解いたり、多方面への研究が行われている。一斉射撃問題の解法では隣接セルの状態を変化させ波のような信号を表現することが重要となる。発見されている解では速さの異なる二つの信号を交差させることにより中心を見つけ、左右で再度中心を見つけ分断していくことで再帰的にすべてのセルを中心状態にしている。 本研究では一斉射撃問題の別視点からのアプローチとして中心を求めずに射撃状態へと遷移するアルゴリズムを考え、これをNetlogo言語で実装し、評価を行った。
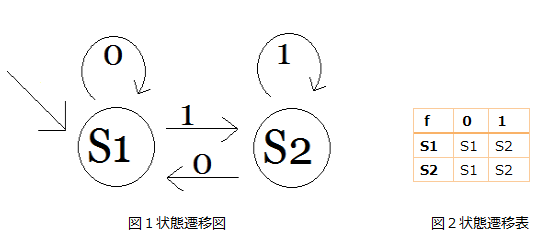
オートマトンとは初期状態から開始され、ある内部状態に対してある値が入力されると、どのような状態に遷移するのかというシステムである。[2] 図1は簡単なオートマトンの例、図2は入力の遷移を表している。今回は初期状態にS1を与えている。

図2から以下のことがわかる。
時刻tの状態をS(t)入力をa(t)と書くと(1)式が成り立つ
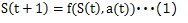
また、例ではS1とS2の2つの状態が存在していたので状態数2のオートマトンという。
セルラーオートマトンとは、格子状のセルにオートマトンを配置し、隣接セルの状態を入力として状態遷移をするものである。また、セルラーオートマトンではセルが一列に連なっている1次元セルラーオートマトン、セルが縦横に並んでいる2次元セルラーオートマトンがある。1次元の場合では、あるセルの次の状態が、セル自身と両隣にある2つのセルの3つによって次の状態を導き出す3近傍を用いられることが多い。 つまり時刻tのi番目のセル状態をCi(t)とすると、各セルの状態遷移は遷移関数fは(2)式のように表せる。
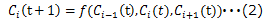
である。
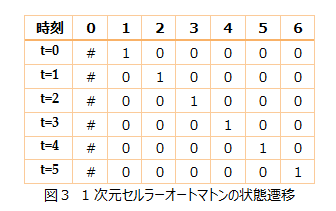
図3は1次元セルラーオートマトンの時間経過による状態遷移を表している。セル上部の数字は左から何番目のセルに位置しているかを表しており、各セルに書かれている数値はそれぞれのセルの内部状態を示している。セルが0番目の#は兵士のいない状態を表しており、決して状態が変わることがない。t=0で初期状態を与えておりt=1での二番目のセルの状態はt=0での1,2,3番目の3つのセルの状態により算出される出力で決定する。つまりf(1,0,0)=1という遷移規則を持つ。このような遷移規則に従い全てのセルが一斉に変化する。 また、このある状態が横に移動していることを波と捉えて速さ1の波と呼ばれ、一斉射撃問題ではこの波の考え方がとても重要となる。
一方二次元の場合では、あるセルから見て上下左右と自身の5つのセルによって次の状態を算出するノイマン近傍と、ノイマン近傍に加えて斜めにあるセルも含めた9つのセルにより算出するムーア均衡の2つの算出方法がある。

なので、式に表すと、
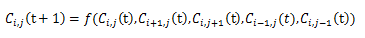
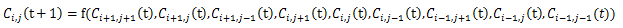
となる。
一斉射撃問題とは任意個数のセルラーオートマトンが同期し、一つのオートマトンだけが特別な状態になった後、すべてが同じ状態へと遷移するアルゴリズムを見つける問題である。 1957年Myhillにより一斉射撃問題 が提唱された。Minskyらにより世界で最初の3n+o(log n)ステップ(nはセル数を意味する)の一次元一斉射撃アルゴリズムが提案される。このときは最小時間解は求められていなかったが、1961年に後藤英一が先頭から出された信号が列を往復する時間(2nー2ステップ)だけで一斉射撃できることを示した。その後1966年にWaksman[1]が16状態の有限オートマトンによる最小時間解を示し、1967年にBalzerが8状態による最小時間解を示した。さらに1987年にはMazoyerが6状態による最小時間解を示している。
John MacarthyとMarvin Minsky は世界で始めて一斉射撃問題を解いた人である。内部状態数15によって兵士の数をnとしたとき、3nステップで射撃状態に遷移している。
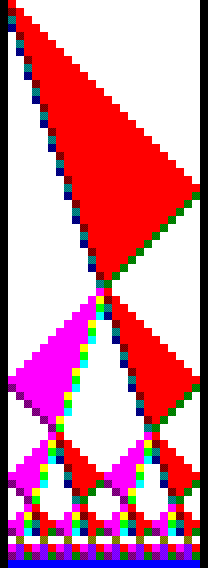
図7はMinskyらによるアルゴリズムを示している。横軸が兵士の数で、縦軸は時間軸を表しており、下に行くほど時間が経過している。各セル内部の色はそれぞれの内部状態を示しており、異なる色の場合は内部状態が異なる。 まず、一番左の将軍から、速さ1の波と1/3の波を同時に発信させる。速さ1の波は右端に到達時に別の内部状態となり逆方向へ同じ速さで進む。速さ1の波が1.5n進んだときに、1/3の波は0.5n進むので反射した速さ1の波と1/3の波は中間地点である1/2nで衝突する。求められた中心をもとに速さ1と1/3の波を左右に発信させる。これにより先ほどと同様に1/4nと3/4n地点で衝突する。このように再帰的に中間地点を求め続けることにより全てのセルが中間地点と同じ状態となり、その後射撃状態へ遷移する。
Waksmanのアルゴリズムでは16状態によって2n-2ステップで射撃状態へ遷移している。2n-2ステップによる同期は最小時間解とも言われ、これ以上早く一斉射撃状態となる事はないと証明されている。
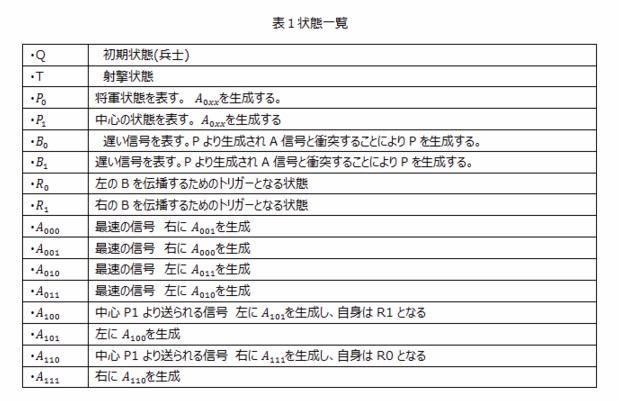
P0P1はブレ射撃状態と呼ばれ、射撃状態になる前に取る状態である。Waksmanのアルゴリズムではセル空間を等しい長さの部分空間に再帰的に二分割するが、このP0,P1は部分空間の境界記号ならびに将軍状態として働き、左右のセルがP0もしくはP1となったときに射撃状態へ遷移する。 B0B1は波信号と呼ばれセル空間上を一定のスピードで進行する波を表現するために使用される内部状態である。A信号と衝突することによって、セル空間をよりサイズの小さい部分空間に分割する。B0B1の2つの状態があるが、これは奇偶性を判別するためである。 R0R1はトリガー信号と呼ばれ、B信号を進行方向へ動かすためのトリガーとして用いられる内部状態。セルラーオートマトンでは全てが状態遷移式によって求めれているため、同じ内部状態を用いて速さの異なる信号を表現する場合、それぞれ動かすためのトリガーとなる状態を設定し、隣接させなければならない。R0とR1はこのトリガーの役割を担う状態である。 Aijk,ijk∈{0,1}の8種類がありそれぞれセル空間を速さ1で伝播する信号の役目を果たし、kの値によって将軍および分割点P0P1から奇数番目なのか偶数番目なのか判別している。jの値は進む方向が右なのか左なのかを表し、iの値はP0から生成されているかP1から生成されているかを表している。

図8はWaksmanのアルゴリズムのシミュレーション結果である。長さ11のセルを20ステップにて射撃状態へ遷移している。 A01xによって最速の信号を将軍から右端に送りつつRをトリガーとしてBは1/2m-1(m>2)ステップで進む信号を表現している。このR信号はA信号が奇数番目の時生成され、A信号とは逆方向へ進みBと衝突する。衝突したBは1マス進みR信号はB1と衝突したなら消滅、B0なら生存する。Pに衝突した場合はB0を生成し、B信号を複数生成させている。なので、このR信号によりB信号は永続的に作られ続け、さらに生成されるたびに遅い信号となっていく。 A01xは反射して逆方向にA00xとして返ってきてBと衝突しP1に遷移する。P0とP1は準射撃状態として左右がP0またはP1の時に射撃状態Pとなる。 なお、このアルゴリズムは近年,状態遷移規則に誤りがあるということが示されている。[3] このアルゴリズムは遷移規則数3208で行っているが、近年の誤りの指摘によって202まで減らされた。
二次元一斉射撃問題だと、一般的にセルが正方形の場合と長方形の場合が多く研究されている。正方形n×n(n>2)の場合は2n-2ステップ9状態の同期アルゴリズム[4]、長方形n×m(n,m>2)の場合はn+m+max(n,m)-3ステップ28の同期アルゴリズム[5]や2(n+m)-4ステップ6状態の同期アルゴリズムが知られている。[6] 例としてサイズn×mのセル空間を考える。
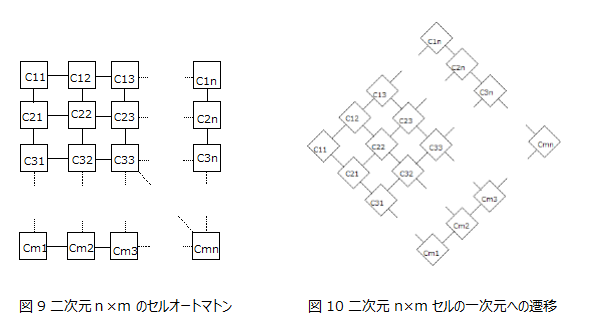
図9はn×mの二次元セル空間を表している。Cnmは、左からn番目、上からm番目のセルであることを表し、直線により繋がっているセルはそれぞれ次の状態に遷移する際に参照とするセルを表している。図9はノイマン近傍であり、セル一つに着目した場合、次のセルの状態は上下左右中央のセルを参照し状態遷移する。たとえばC2,2に着目した場合
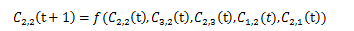
と表せる。これを図10のようにセル空間全体を斜めにして表し、同じ縦列のセル全てをまとめる。 配列gとし
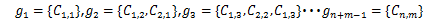
とすると
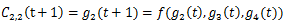
となり、これは一次元セルラーオートマトンでの3近傍の式となる。 なので、二次元での上と左、右と左をそれぞれ一次元での左、右として考え遷移式を当てはめる事により一次元セルラーオートマトンとして考えることができる。このため全てのセルは壁を考慮しつつ上と左、右と下は同じ状態である時に出力するように状態遷移式をしなければならない。
従表示されてきたように一斉射撃アルゴリズムのほとんどは中心を求めている。これは中心を求めることにより右側と左側に同じ信号を流すことで、再帰的に中心を求め続け一斉射撃問題を解く為である。このため状態数を少なくすることができる。 本研究では中心を求めずに一斉射撃問題を解く。今回は将軍の位置は左端固定の1次元セルオートマトンとする。
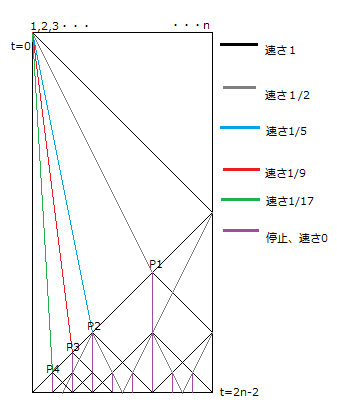
3.1節より中心を求める場合は速さ1の最速の信号と速さ1/3の信号の衝突点により求められてる。今回は中心を求めずに射撃問題を解くので速さ1/3の信号は用いず1/2,1/5の信号を用いる。これにより、図11のように点P1P2において衝突する。また、速さ1の信号が端に到着時に同様に左側に1/2のトリガー信号を送る。すると1/3,2/3を同時に起動させることが可能である。また、点P1P2の起動時に左右の端点より信号を送る事で、短時間で射撃状態へ遷移することができる。しかし初期状態が将軍であった左端には右端に到達し反射した信号が戻ってきていないので、トリガーが無く信号を送ることができない。なので速さ1/2,1/5の信号を送る際に同時に速さ1/9,1/17の信号を送る。これにより速さ1の信号と2/9,1/9地点で衝突する。これにより9分割することが可能である。
一斉射撃アルゴリズムの正当性を確認するに当たり、NetLogo言語を用いた。Netlogoは処理系として二次元セルラーオートマトンを含んでいるのでこの機能を用いる。 このNetLogoを用いて将軍左端固定の1次元同期アルゴリズムにおいて状態数27、遷移規則数73、2n-2ステップで射撃状態へ遷移した。 今回は速さ1,1/2,1/5の信号のみを発信させている。これにより同期する長さが制限される。 信号の速度を遅くさせる方法として、1ステップごとに状態を変化させ、1,4ステップ経過したときに一マス進み状態を戻し、また状態を変化させて一マス進み・・・という方法を行っている。
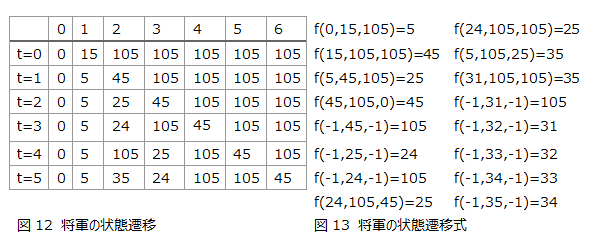
本研究ではNetlogoをもとに状態を設定しているので内部状態は数値にて表す。105は兵士、15は将軍である。下一桁は遅い信号および逆方向同速度の信号を使う際に用いている。下二桁目が異なる場合は用途の異なる状態である。0は壁を表し兵士はいない。 またNetlogo言語において-1は任意の数値である。そのため状態遷移式での-1はどの値が入力された場合でも宵ということとなる。ただし、複数の同じ入力から異なる出力が定義される場合、先に定義している式を優先する。 また、右に進む場合と左に進む場合も別の状態を使っている。 図12は将軍の状態遷移、図13は状態遷移式を表している。将軍は速さ1,2,1/5 の信号を生成している。遅い信号は各ステップごとに状態を変化させ、一定の時間がたった後に横へ移動するように遷移式を組み立てている。 また、最速の信号が右端到達時に速さ1と1/2の信号を送るようにする。
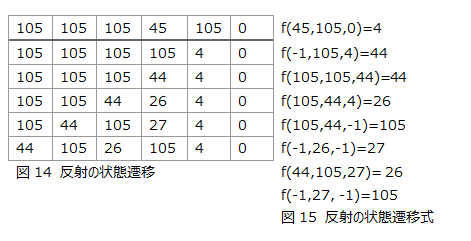
図14は反射時の状態遷移、図15はその遷移式である。端点到達時に状態を変更し逆方向へ内部状態44の速さ1の信号を送っている。遅延無く速さ1/2の信号を送るため44は26へと遷移し2ステップごとに右に進む。
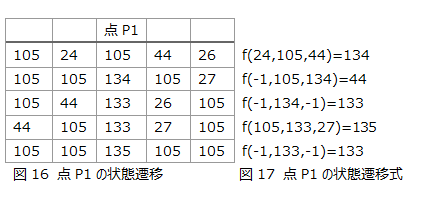
1/2の信号と反射してきた速さ1信号の衝突点をP1、1/5と1の衝突点をP2とする。P1は左に最速の信号を流し静止する。 速さ1/5と-1の信号の衝突時にP1を動かすためP1に1/2 の信号が到着時に起動するようにする。これによりP1とP2が同期する。 2点で同期した後は左右に1,1/2 の信号を発信させる。これにより、それぞれの面での2点を求め続けることとなり。一斉射撃状態となることができる。また、関連研究同様二次元上での同期することができる。

図18 は一次元長さ10のときの同期アルゴリズムをNetLogoで実行した例である。図では縦軸を時間軸とし、下へ進むにつれて時間が進んでいるように表しているが、実際はクリックにより時間が進み射撃状態へと遷移する。
本研究ではセルラーオートマトンの同期アルゴリズムである一斉射撃問題について研究し、普段行われていない中心を求めない一斉射撃問題の解法を模索した。今回は1次元且つ将軍を端固定と定義し、その結果長さ10において18ステップで射撃状態へ移行することができ、これにより中心を求めずとも射撃状態へ遷移することができるということが確認できた。本研究で求めた点P1は中心が求まるよりも早い時間で求めることができる。これを活かすことによってより良い解法を探すことが課題である。また、別の見解として二次元セルラーオートマトン上において近年一次元への近似を行わないアルゴリズムも増えてきている。本研究を織り交ぜることによって、より速いステップにて一斉射撃問題を解くことができないか考えていきたい。また本研究の改善点として、長さnの場合でも同期ができるよう、信号を永続的に発信させる方法。また、将軍の初期位置が端以外の場合でも同期ができるようなアルゴリズム、状態数を少しでも減らせないか考えていきたい。
今回作成した、1次元27状態3近傍の同期アルゴリズムで用いたルールを以下に示す。なお、数字は状態を表すが、-1はどの状態が入力されてもよいとする。ただし、Netlogo言語では複数の同じ入力から異なる出力が定義される場合、先に定義している式を優先する。
