
図1.数独
「ニコリ」というパズル雑誌で考案された「橋をかけろ」というパズルがある。その「橋をかけろ」の一般化問題がNP完全問題であることを、既知のNP完全問題「次数3の頂点からなる平面無向グラフにおけるハミルトン閉路問題」から多項式時間還元することで証明されている[2]。しかし、その証明では多項式時間に関する厳密性が欠けていた。本研究ではこの証明を厳密に行った。
ペンシルパズルとは大前提として一般に「完全情報パズル」であると認知されている。つまり運の要素がない。問題は紙に描かれた図の形で与えられ, その上に鉛筆(筆記具) で何かを書き込むことで問題を解くという形式である。但し、問題を解くのに, 与えられた図の領域以外の大量の領域を必要としないなお、虫食算、覆面算は通常整数解の連立方程式を解くことになるため大量の計算用紙を必要とすることが多い。そのため、この要件を満たさないとされている。
図1は有名な数独(Sudoku)と呼ばれるペンシルパズルである。

図1.数独
空いているマスに1?9のいずれかの数字を入れる。但し、縦・横の各列及び、太線で囲まれた3×3のブロック内に同じ数字が複数入ってはいけない。これを解くのは一般には整数の連立方程式になるが、この重複を許さないという条件をうまく使うことで大量の領域がなくても解くことができる。図1では中央の列において4がどこかに入るかを考えると、空いている3マスのうち一番下は、太線内にすでに4があるため入れられず、また中央は横の行を考えるとすでに4がある。従って、上の空いているマスだけに4を入れることができる。このようにうまい着眼点を見つけることにより、少ない選択肢を吟味することで答えを順に確定していける点がこのパズルの面白さといえよう。
図2はカックロ(加算クロスの略)と呼ばれるペンシルパズルである。
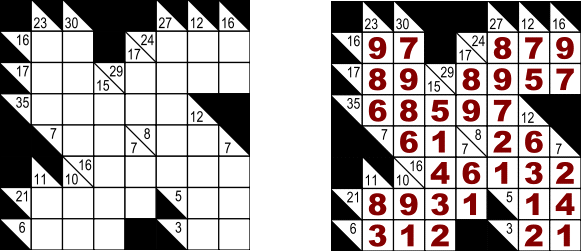
図2.カックロ
各四角いマスに 1〜9 の数字を入れる。ここで斜めに仕切られたマスにある数字のうち、右上にある数字は横へ続く空マスの計。左下にある数字は縦へ続く空マスの計を表す。ただし、縦横に連続する空マスの中に同じ数字は入らない。 これは重複を許さないというルールのより、定石が数多く存在する。例えば、2マスのみの場合3であれば1+2か2+1のみ(これを(1,2)で表す)。4も(1,3)のみ。また17は(8、9)のみ。16も(7,9)のみである。 図3では一番左上の16は(7,9)である。一方23は(6,8,9)のみなので共通の数字は9しかない。従って一番左上は9が入る。 カックロは多くの定石を2つずつ組み合わせて、共通の数が1つになる場所を求めていくことで解いていく。
図3にスリザーリンクと呼ばれるペンシルパズルを示す。
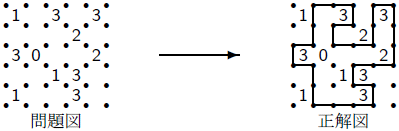
図3.スリザーリンク
盤面は格子をなす点の集まりとして与えられる。点の全体は長方形をなしている。格子の単位長を1とした時、その長方形の縦横の長さのことを盤面のサイズという。 4点に囲まれた1×1の正方形のことを面という。面には0,1,2,3のいずれかの数字が書かれていることがある。 目的は、格子上で隣接する(距離が1である)2点間に線を引いて、次の条件を満たす1つの輪(初等的な閉路)を作ることである。(隣接する点の間の、線が引かれうる領域のことを辺という。)
このパズルはルールがシンプルである割に様々な定石があるため、経験を積むと解く力が上達していく。また線は交わらないため、解が埋まっていくに連れ盤面が分割、限定されるため、単なる経験だけでは解けない点を魅力と言えよう。 図2においては簡単な定石として30の対や33の対が見られる。また、1や3が角にあると、線が引ける場所が限定される。
問題が難しいとか易しいとかを、議論するにはどのような手法を使えば良いのだろうか?なお、ここでいう問題とは、「双子素数は存在するのか?」など個別にyesかnoを答えるものではなく、「実係数方程式の実根の存在性」のようなパラメータにより無限個の例題が作れるものを扱う。さらに答えがyesかnoのみの問題に限るとする。 さて、易しいことを示すには、実際に手順の少ない解法を示せば良い。例えば二次方程式の実根の存在性については、解の公式により解を求め、実根かどうかを判定すれば良い。 しかし、難しいことを示すにはどうすれば良いのだろうか?ここで還元可能性という概念を考える。
あるyesかnoを判定する問題Aの例題xを別の問題Bの例題yに簡単な手順で変形できるとする。このときAの解法として例題xを直接yes、no判定する方法とAにおけるxをyに変形してからBにおけるyの解法を使う方法がある。ここでAとBの難しさを考えるとBが解けてしまえばAが解けることになるので、Aの難しさはせいぜいBを解く程度となる。例えば、「実係数二次方程式の実根の存在判定問題」(Aとする)に対して、「実数yの非負判定問題」(Bとする)を考える。 ここでAの例題としてax2+bx+c=0が与えられたときyとしてb2-4acを与えると、Bの判定(つまり非負判定)をするだけでAが解ける。この場合Aの難しさはせいぜいB程度となる。このように、問題の例題を変換できることを還元可能性という。この性質は、反射律、反対称律、推移律を満たすので半順序になる。従って、A≦Bで表す。
さてここでもし、解くのが難しいと思う問題Aと、未知の難しさの問題Bについて、このA≦Bという関係が成り立った場合、BはAと同等かそれより難しいと言える。つまり、難しい問題の例題を未知の問題の例題に変換することは、その問題の難しさを議論していくことになる。
計算理論において多項式で表される計算時間。多項式時間のアルゴリズムとは、解くべき問題の入力サイズnに対して、処理時間の上界としてnの多項式で表現できるものが存在するアルゴリズムを指す。問題入力サイズの増大に対する、処理時間の増大を表すものである。 たとえばバブルソートの処理時間は要素数nに対して要素の比較・交換を行う回数は高々1/2 n(n-1) である。 したがって、この場合の最悪計算量のオーダーはO記法を用いてO(n2)と表される。 またクイックソートの期待計算量のオーダーはO(n log n)、最悪計算量のオーダーはO(n2)である。
本研究で扱う問題は無制限の例題を持つようなものとする。 そして、各例題はyes、noの区別があり、問題Aの例題xがyesであることをx∈Aと書く。 複数の問題を扱うとき、特定の性質を持つかどうかで分類する。 これを問題のクラスと言う。ある問題Aの例題aが決定性多項式時間決定性チューリング機械で別の問題Bの例題bに変換でき、a∈A⇔b∈Bを満たすとき、これを、多項式時間の還元可能性をA≦mpBと書く。これは直観的にはBの解法があればAの解法を作ることができるのでAはBほど難しくないことがわかる。
これの閉じた最小のクラスをPとする。Pに含まれる問題は全て多項式時間で解ける。また、完全情報パズルなどある種の組み合わせ最適化問題は、非決定性チューリング機械で多項式時間で解けるクラスに属する。これをNPと呼ぶ。
非決定性のプログラムであっても、全て数え上げができるため、問題AがNPに属するときAの例題xに対してAを解く非決定性のチューリング機械の番号iと、ある定数nに対して、問題Bを(x,i,n)に対して、「プログラムiが|x|n+n時間以内に入力xに対してyesを出す」とすると、A≦mpBとなる。このような、クラス内のすべての問題から還元可能性な問題を完全問題と言う。 この場合、BはNP完全問題である。
Cookの定理とは和積標準形の論理式で非決定性のプログラムが作れる真になる変数割り当てがあれば解けることがわかる定理である。SATがNPに入ることは明らかである。正解となる論理変数の割り当てを知っていれば、節が充足されることを検証するのは簡単である。 SATがNP完全であることを示すには、NPに属するあらゆる問題が、SATの一例とみなせることを示さなくてはならない。しかし、あらゆるNP問題を逐一SATに変換していては埒が明かない。 そのかわり、非決定性チューリング機械の全動作パターン、すなわち、多項式時間で終了するあらゆるプログラムをSATで特定できることを示す。
ハミルトン閉路問題とは、与えられたグラフについて、全ての頂点を一度だけ通る閉路が存在するかどうか調べる問題である。与えられたグラフが有向グラフの場合は有向ハミルトン閉路問題、無向グラフの場合は無向ハミルトン閉路問題と呼ばれる。この問題はどちらも、NP完全問題であることが知られている。また、無向ハミルトン閉路問題は巡回セールスマン問題の特殊ケースでもある。始点と終点が一致するという閉路の条件を取り去ると、ハミルトン路問題になる。
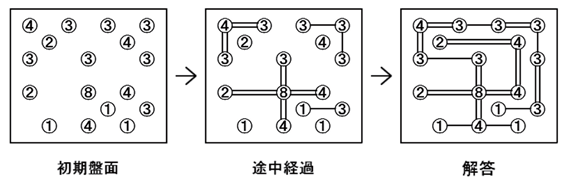
図4.橋をかけろの例題
数字から数字に橋をかけて全体をつなげる。数字は、その数字につながる橋の数である。橋はタテヨコにのみかけることができ、ナナメにかけたり、数字を飛び越えたりすることはできない。但し、橋は1箇所に2本までかけられる。又、橋同士が交差してはいけない。
「橋をかけろ」の一般化問題を『n×nの盤面上で「橋をかけろ」のパズルが与えられ、パズルに解が存在するかどうかを決定する問題』と定義する。この「橋をかけろ」の一般化問題がNP完全問題であることを証明するために、次の2つの性質を証明する。
まず、1つ目の性質について考える。パズル「橋をかけろ」は、盤面上の各数字に対して橋をかける位置と本数を非決定的に推測し、かけた橋が解になっているかを調べればよいので、この問題はNPで解ける。 次に2つ目の性質について考える。既知のNP完全問題「次数3の頂点からなる平面無向グラフにおけるハミルトン閉路問題」が、パズル「橋をかけろ」の一般化問題に多項式時間還元可能であることを示す。はじめに小松原の結果[2]を示す。 次数3の頂点からなる平面無向グラフGが与えられたとする。Gから「橋をかけろ」の一般化問題の入力となる盤面上の数字の配置を次の手順で構成する。
Gのすべての頂点に対し次を行う。「橋をかけろ」ではナナメに橋をかけることができないので、図5 のような次数3の頂点xに隣接する辺を、図6のように頂点に対し辺が垂直に接続するように変換する。この頂点を、図7のように数字を置いて変換する。これを「頂点構成」と呼ぶことにする。盤面を構成する際には、残りの1辺には他の数字から橋がかからないように配置する。
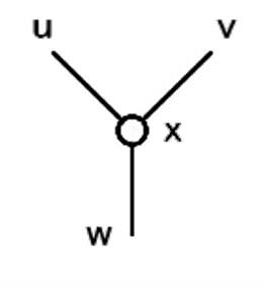
図5.次数3の頂点
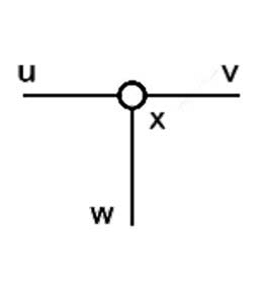
図6.変換後の頂点
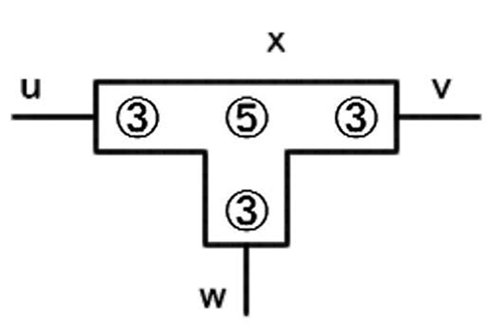
図7.頂点構成

図8.盤面上の配置
Gのすべての辺に対し次を行う。前セクション同様にナナメに橋をかけることができないので、図9のような頂点間をつなぐ辺e=(u,v)にを、図10のように垂直方向の折れ線または直線に変換する。このような辺を、図11のように数字を置いて変換する。これを「辺構成」と呼ぶことにする。e部は2つで、e、e部は0〜偶数個で構成される。数字は辺の形状にあわせ垂直方向に配置する。盤面を構成する際には、辺の構成として繋がりあう数字以外の数字から橋がかからないように配置する。
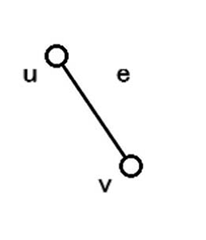
図9.ナナメの辺
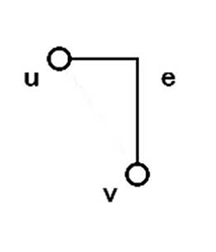
図10.変換後の辺
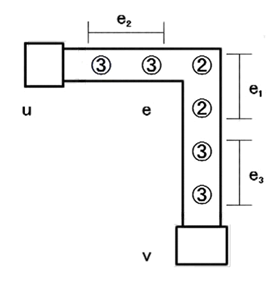
図11.辺構成
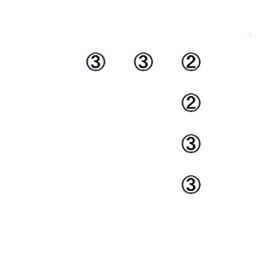
図12.盤面上の配置図
以上の変換を用いると、例えば図13のような次数3の頂点からなる平面無向グラフに対して、変換したグラフは図14、構成した盤面は図15、図16のようになる。
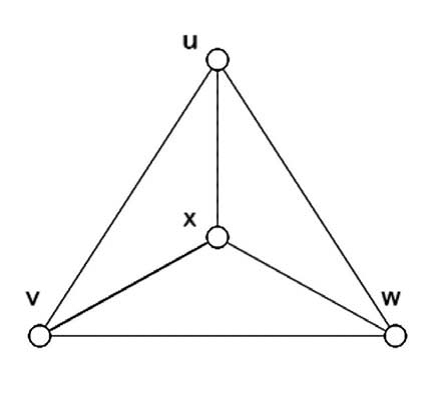
図13.次数3の平行無向グラフ
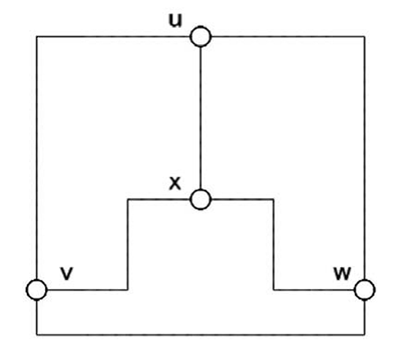
図14.変換したグラフ
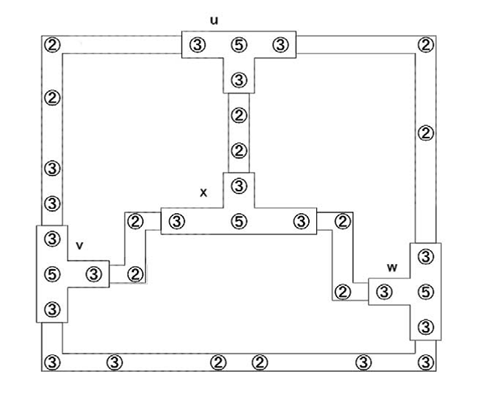
図15.図14より構成した「橋をかけろ」の一般化図
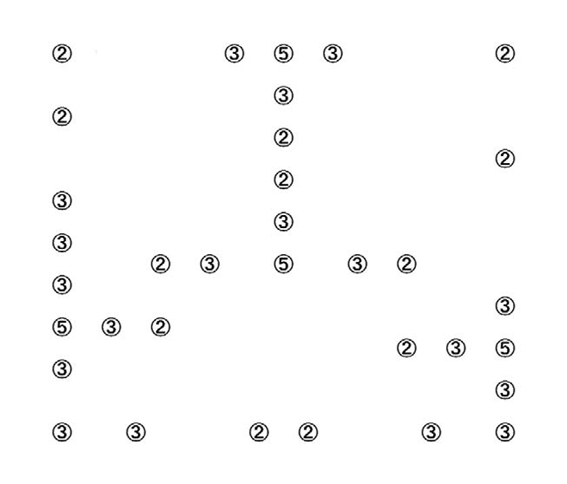
図16.盤面としての図
これを示すのに次数3の平面無向グラフにおけるハミルトン閉路問題の例題を、「橋をかけろ」の例題に変換する必要がある。この問題の入力は3頂点の平面グラフである。これを「橋をかけろ」問題に変換する。
構成した「橋をかけろ」の一般化問題が解を持つための必要十分条件は、「次数3の頂点からなる平面無向グラフにおけるハミルトン閉路問題」の解が存在すること、を示す。
Gにハミルトン閉路Cが存在すると仮定する。Cに対応して、次のような「橋をかけろ」の解が存在することを示す。Cに辺e=(u,v)が含まれないとする。 このeに対応する辺構成を、図19ようにe部で切り離す。 「橋をかけろ」のルールでは、すべての数字が橋でつながらなければいけないので、数字が孤立しないように頂点構成へ繋げる。このとき、数字からは同一方向へ2本の橋がかかり、頂点構成へも2本の橋がかかる。
逆に、Cにeが含まれるとする。このeに対応する辺構成は、図20のようにすべての数字がつながるように橋をかける。このとき、数字からは別の方向へ1本ずつ橋がかかり、頂点構成へかかる橋も1本である。
上記のようにすべての辺構成について橋をかけ、残りの構成に対し「橋をかけろ」のルールに沿って橋をかけると、すべての数字が橋でつながり、構成した「橋をかけろ」の一般化問題に解が存在する。よって、 にハミルトン閉路が存在すると、構成した「橋をかけろ」の一般化問題に解が存在する。
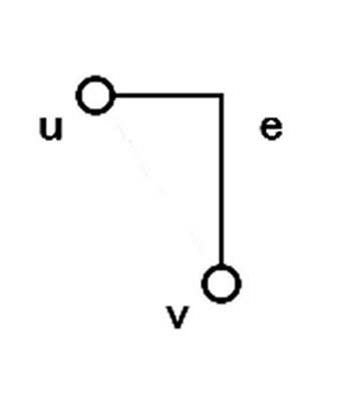
図17.辺e=(u,v)
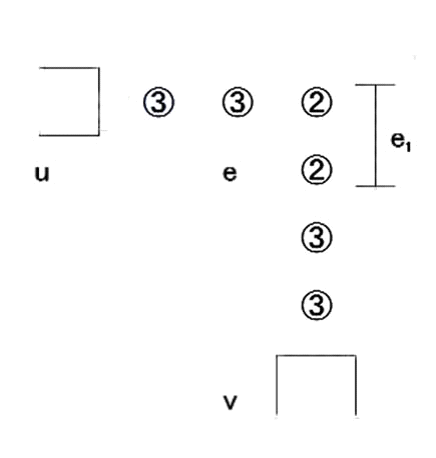
図18.図17に対応した辺構成
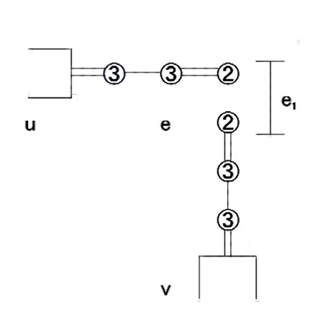
図19.Cに含まれないeに対応した辺構成の橋のかけ方
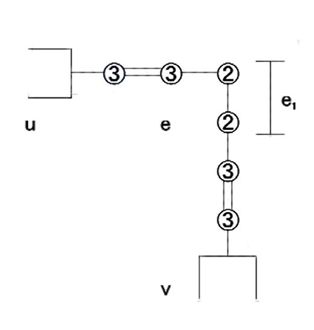
図20.Cに含まれるeに対応した辺構成の橋のかけ方
次に、構成した「橋をかけろ」の一般化問題が解を持つと仮定する。このときにハミルトン閉路が存在することを示す。 図21のような次数3の頂点xと隣接した辺に対応した、図22、図23の構成について考える。
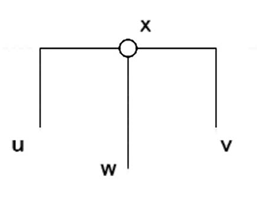
図21.次数3の頂点と隣接辺
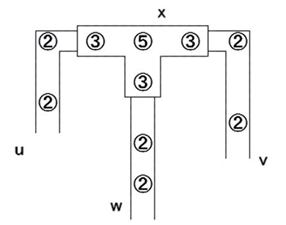
図22.図21に対応した構成
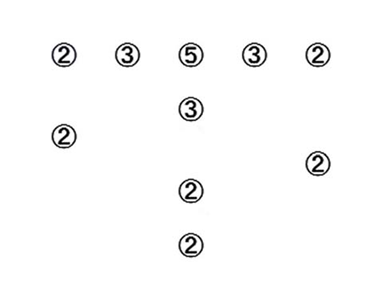
図23.盤面上での配置図
図23の構成において、図24、図26、図28の3通りの橋のかけ方が存在する。それぞれが図21における頂点の通り方に対応している。
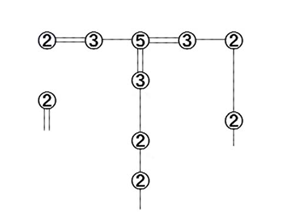
図24.左側で辺構成を切り離した場合
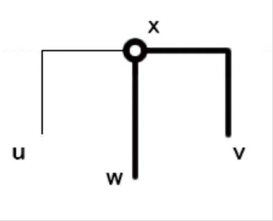
図25.図24の場合の頂点の通り方
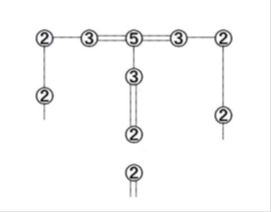
図26.下側で辺構成を切り離した場合
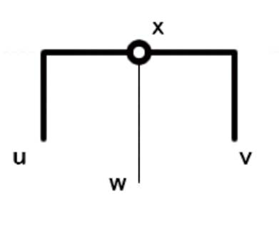
図27.図26の場合の頂点の通り方
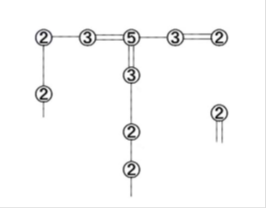
図28.右側で辺構成を切り離した場合
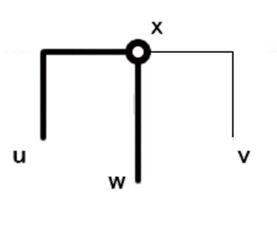
図29.図28の場合の頂点の通り方
図24のように左側で辺構成を切り離した場合、Gでは図25のように右側と下側の辺を通って頂点を通過する。 図26のように下側で辺構成を切り離した場合、Gでは図27のように左側と右側の辺を通って頂点を通過する。 図28のように右側で辺構成を切り離した場合、Gでは図29のように。左側と下側の辺を通って頂点を通過する。 いずれも構成に橋をかけることが可能であれば、Gにおける頂点を正しく通ることが可能である。 よって、構成した盤面に解が存在したときに出来た閉路は、上のハミルトン閉路である。
さて、小松原の証明はここまでである。 元のハミルトン閉路のサイズがNであった時、この還元された「橋をかけろ」の問題のサイズがどれくらいになるか見積もる。ここで問題なのは、橋をかけろの例題において、頂点同士はいくら離れていても接続できるここである。したがって、機械的にガジェットを配置すると、相互に関係してしまう。そこでガジェットを少しずつずらして配置すれば良い。N個中k番目のガジェットを(x,y)座標に配置する場合(Nx+k,Ny+k)に配置すれば良い。このようすると問題のサイズは元のN2倍であるが、これは多項式である。
本研究では小松原の「橋をかけろ」のNP完全性の証明において、還元された問題のサイズを正確に求めた。その結果、構成した「橋をかけろ」の一般化問題の一辺の長さは、G中の頂点と辺の個数の和の高々3乗なので、一般化問題の構成は多項式時間で出来る。 よって、パズル「橋をかけろ」の一般化問題のNP完全性が証明された。