
図 2.1 時間―距離平面上での 1 分間交通量×平均速度(運動エネルギー)に よる粗密波の濃淡表示(首都高速道路 1 号線上り)
03kc085 平石 隆洋
指導教員 坂本 直志 助教授
蟻や、蜂などの集団行動は、一見すると非常に複雑な振る舞いをする。 例えば、採餌行動において、近くの餌場に集団で集まり協調しながら巣に餌を 運ぶなどの行動において、蟻同士が互いに対話を行い、餌場に集結する行動が 見られる。 これらの行動は蟻が高度な知能を備えており、状況判断や協調という概念に基 づいて行われると解釈することもできるが、その一方、「群知能」という考え 方で見ることもできる。 これは個々の個体自体は単純な機能しか持ち合わせていなくても、多くの個体 が集まることにより、相互作用として全体として知的で高度な行動が可能にな るという考え方である。 このことは後で詳しく説明する StarLogo システム上での単純なプログラムに よるシミュレーションという形で、解釈することができる。
StarLogo とは Logo システムが元になっているシステムである。 Logo とは一種のプログラミング言語であるが、グラフィックディスプレイを 前提とし、タートルグラフィック機能を実現している。 このタートルグラフィックとはタートルと呼ばれるカーソルが画面上にあり、 タートルの向きや移動方向をあたえると、軌跡をグラフィックとして描くもの である。 Logo は、この他、Lisp 同様にリスト表現や無名関数などを持つ。 Logoは、教育用として開発された言語であるが、表現力が高い。 この Logo に対して次のような拡張をしたのが StarLogo と呼ばれているもの である。
このような StarLogo は、蟻の採餌行動などを簡潔なプログラムによりシミュ レートすることができる。
MIT の StarLogo プロジェクトにおいて高校生たちとの共同研究により、さま ざまな群の振る舞いのシミュレーションが作られた[1]。 これにより、一見複雑な群の振る舞いが、単純なプログラムによりシミュレー トできることが分かった。
本研究ではこのプロジェクトの中で行われた自動車渋滞のシミュレーションに 着目した。 高速道路など、直線の道を通行する際には、車の運転はそれほど複雑では無い。 制限速度に合わせて運転し、車間距離が詰まったらブレーキをかける程度であ る。 このような単純な車の運転のルールをプログラムにあたえると、現実で起きて いるような渋滞がシミュレーションでも起きることが分かった。
本研究では、従来から行われている自動車渋滞の解析の結果と照し合せ、 StarLogo による単純なプログラムによる自動車渋滞のシミュレーションが、 実際の自動車渋滞の解析に有用であることを示す。
高速道路で渋滞が発生したとき、気になるのは到着時刻がどれくらい遅くなる かや、実際に渋滞している場所などである。 つまり、渋滞の規模や性質などの情報に興味を覚える。 渋滞情報は、各種道路情報のなかでも道路利用者にとって最も関心の高い情報 であり、その高い検出精度が要求されている。 しかし、渋滞とは定常的なものではない。 渋滞内の自動車は常に入れ替わり、また、渋滞箇所や長さは変動している。 そこで、渋滞の性質などの予報が必要となる。
さて、渋滞とは車が集団で徐行する現象であるが、コンピュータで取り扱うた め、本研究では「先行車によって速度を制限された状態」として扱うとことと する。
また、通常の研究で使われている用語や考え方をここで整理しておく [2][3][4]。
自動車交通流の特性を把握するために、次の巨視的状態量が用いられる。
交通量(volume;
密度は、道路の距離軸上での状態量であり、単位延長の道路上に存在する車両
の数をいい、通常 1 kmあたり存在台数(台/km)で表される(それより長い、
短い場合は換算値を用いる)。
時間的に変動するので、交通流率等、他の状態量との関係で交通状態を表現す
る場合は、通常、他の状態量の測定に用いられた集計時間内でサンプリングし
た密度の平均値が用いられる。
密度と関係する個々の車両に着目した微視的な状態量として、車頭距離(
平均速度にはその平均のとり方の違いによって、時間平均速度と空間平均速度
の 2 種類がある。
時間平均速度(time mean speed;
なお、以下において交通流率、密度、平均速度相互の関係を論ずる場合には、
平均速度は特記しない限り空間平均速度(
具体的な渋滞の定義は、交通需要が交通容量を超過した場合に、交通容量極小 の地点を先頭にしてその上流区間の速度が低下し、待ち行列が形成される状態 とされている。 対象道路区間のうちで交通容量が最少となりそこを流れる交通の妨げとなって いる地点を「あい路」(ボトルネック)という。 このとき交通需要と交通容量との差分を超過需要といい、これが渋滞列長など 渋滞の程度をきめる。 実際の交通流での渋滞検出には、平均速度が用いられることが多い。 検出精度は、検出基準(閾値)、平均化のための集計単位時間等によって変わ る。 都市内高速道路を対象とした研究によると、検出のための閾値を平均速 度 45km/h とした場合に検出誤差が極小になることが知られている。
渋滞は発生原因から、自然渋滞と突発渋滞とに分けられる。 自然渋滞とは、道路構造条件のために交通容量が相対的に小さくなっているよ うな地点を先頭として発生するものであり、その容量を超過する交通需要が生 起するたびに、同じ箇所で繰り返し発生する。 一方、突発渋滞とは、交通事故・車両故障などの突発事象によって、一時的に 交通容量が低下するために起きる渋滞である。典型的なボトルネックは、合流 部、トンネル部、カーブ区間、幹線道路どうしの交差点、多枝交差点、サグ区 間(凹部のことで、下り坂から上り坂に変化するところ)、織り込み区間(複 数の路線が合流してから、また分岐するまでの区間)などがあげられる。
渋滞時の交通現象は、非渋滞時とは大幅に性質が異なっており、流体理論等の 従来の理論モデルでは説明しきれないことが知られ、渋滞流を対象とした研究 が積極的に行われるようになってきている。次に、渋滞時の交通流の特性とし て粗密波の空間変動特性について説明する。
渋滞時の交通流は、道路軸方向に沿って必ずしも一様な交通密度の分布状態に あるのではなく、交通密度の高い部分(密部:相対的低速状態)と低い部分( 粗部:相対的高速状態)とが混在する。 粗密波(compression wave)と言われる両部分の境界は時間的に一箇所にとど まっているわけではなく、時間経過に伴って上流へ移動する性質をもつ(図 2 .1 )。 渋滞流の中を前進する車両はこの粗密波の伝搬に伴って加速・減速、時には停 止・発進を繰り返すことになる。 粗密波の伝搬速度は、都市高速道路での分析結果によると、2km/h 程度である と言われている。

セルオートマトン(Cellular automaton、CA)とは、格子状のセルと単純な規 則からなる、計算モデルである。 非常に単純化されたモデルであるが、生命現象、結晶の成長、乱流といった複 雑な自然現象を模した、驚くほどに豊かな結果を与えてくれる。
セルオートマトンは無限に広がる格子状のセル(細胞のような単位)で構成さ
れており、各セルは有限種類の内部状態を持ち、時間が進むと共に内部状態は
変化していく。
また、ここでの時間は離散的(非連続的)なものであり、時刻
例として、ECAの中でも「ルール 184」と分類される 1 次元セルオートマトン を示す。 1 次元セルオートマトンは線状で、あるセルに隣接するセルは 2 個である。 それぞれのセルは 0 と 1 の内部状態をもつものとして、次の表 2.1 のような ルールを与える。
| 時刻 |
111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| 時刻 |
1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
このルールを元に、更新していくと次の表 2.2 のようになる。 なお、左右の端は繋がっているものとする。
| 時刻 | 状態 |
|---|---|
| 01011010111001010110 | |
| 00110101110100101101 | |
| 10101011101010011010 | |
| 01010111010101010101 | |
| 10101110101010101010 |
ECA で得られるパターンは、一様、周期的、進行、繰り返しなどに分類するこ とができる。 ルール 184 は状態を保存する進行パターンとなっていることが表 2.2 からわ かる。 これは 3.4 で詳しく説明する交通流モデル ASEP の基になっているルールで ある。
また、ルール 184 と呼ばれる理由は、表 2.1 の時刻
本研究で使用した StarLogo システムについて説明する。 グラフィック画面上にタートルを表示でき、また、タートルの移動範囲のバッ クグラウンドにパッチと呼ばれるセルオートマトンがある。 さらに、これらから情報を得て情報処理を行うため、全権的にタートルやパッ チをコントロールする、オブザーバと呼ばれる操作がある。
StarLogo ではこの「タートル」「パッチ」「オブザーバ」についてプログラ ムを行う。 オブザーバが主プログラムになるが、オブザーバで発生させた全てのタートル はタートル用のプログラムに従う。 また、画面上の全てのパッチはパッチ用のプログラムに従う。
プログラムは関数を定義することにより行う。 関数定義の方法は独特である。 「to 関数名」ではじまり「end」で終わる。 コマンドは行単位に書き、また、list は [ ... ] と角括弧でくくり、要素は 空白で区切る。 list 内には通常のコマンド構文が書け、プログラムはこのコマンドの書かれ た list を取り扱うこともできる。
なお、この研究で使用したおもな StarLogo のコマンドの機能は以下の通りで ある。
タートルの数を返す。
指定した状態が真のタートルの数を返す。
指定した数のタートルを生成し、指定したコマンドを実行させる。
呼ばれたタートルから指定した座標までの距離を返す。
タートルが数値分、前進する。
グローバル変数を作る。 オブザーバ、もしくはタートル処理の始めに宣言しなくてはならない。
条件が真のときにコマンドリストを実行する。
条件が真の時にコマンドリスト1を実行し、もしそうでなければコマンドリス ト2を実行する。
ローカル変数を宣言して数値を代入する。 全てのローカル変数の名前はコロンで始まらなくてはならない。 いくつか変数を宣言したい場合、let を次のように書けばよい。
let [:variable1 value1 :variable2 value2]
数値を整数にして返す。
既に宣言されている変数に代入する。
タートル変数を定義する。 オブザーバ、もしくはタートル処理の始めに宣言しなくてはならない。
呼ばれたタートルは、指定した状態が真になるまで待ち続ける。
渋滞は個々のドライバーが集まって起きる物であり、ドライバーの個性により 現象が異なる。 但し、一般には大量のドライバーが集まると、平均的な振る舞いに支配される ことが多いので、渋滞もマクロ的(流体力学など)を用いて解析する手法がある。 本章ではそれについて紹介する。
まず交通流の基本的な性質から説明していく。
交通流の速度を空間平均速度で表せば、個々の車両の速度にばらつきがあって
も、交通流率(
式(3.1)の証明
道路上に小区間
となる。
一方、交通密度
となる。よって式(3.2)と式(3.3)より、
となり、結局、式(3.1)が成立する。
なお、 3 つのパラメータが従属関係にあるだけなので、2 つのパラメータに 対しては別の関係がある。
次節と次々節ではそれぞれ
道路が混雑して交通密度が増えてくると、車間距離が短くなるため、各車は速 度を低下せざるを得なくなる。 次の図 3.1 は、阪神高速道路での速度と密度の測定結果を示したものである。
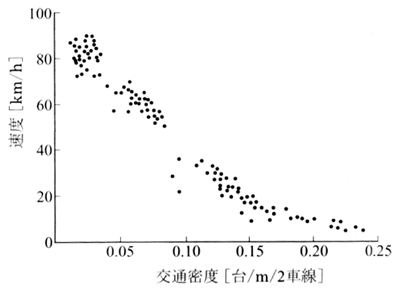
この
これらの定式化の過程を通して得られた、代表的な式と曲線を次に示す(図 3 .2)。
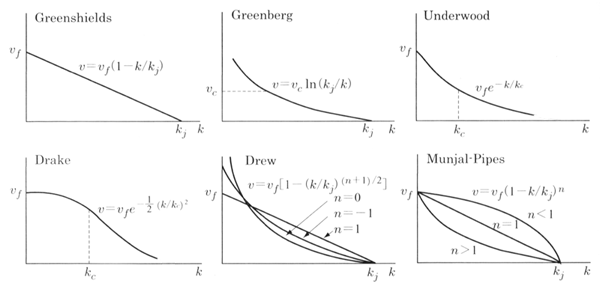
以上の式において、
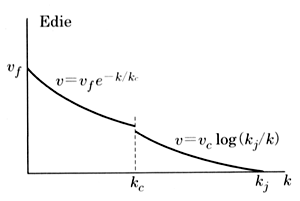
また、モデルの適合性に関する検討事項の一つとして、密度がゼロ付近および 飽和密度における次のような境界条件がある。
前節では、平均速度と密度の関係について着目した。
本節では、交通流率(交通量)と密度の関係に着目する。
これは、
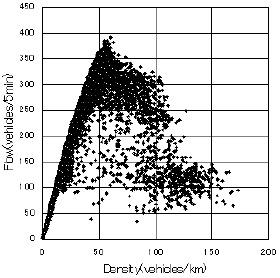
密度が低い、つまり渋滞していない左半分のデータは、右上に伸びる直線状の データとなっている。 これは自由流相であれば台数が増えるほど、ある地点のセンサ上を通過する車 の数も増えるためである。 つまり低密度の領域では、車の密度と流量は比例し、その傾きは平均的な自由 流相での速度をあらわす。 右半分は渋滞流相をあらわし、台数が増えると車間距離が狭くなり速度が低下 していくため右下がりになる。 ただし、実測値からわかるようにその振る舞いは一定ではなく、広がったデー タ分布を示す。
ここで、これまで記してきた交通流の特徴を、この
また、従来から上に凸の一つの曲線で代表することが多く行われてきたが、図 からもわかるように、自由流相と渋滞流相とにそれぞれ右上がり、右下がりの 別個の不連続な相関関係、つまりギリシャ文字のλを裏返したような形 (逆ラムダ型 )になるような傾向もある。
マクロ的に渋滞を考える上で、性質が良いとされている理論モデルが ASEP (Asymmetric Simple Exclusion Process)である。 2.2 で説明したセルオートマトン、ECA のルール 184 モデルを基にしたもの で、車の動きを模して粗密波の伝播などの現象も確認できる [5][6]。
初めにたくさんの箱をずらりとまっすぐに並べ、適当にいくつかの箱に玉を入 れる(入るのは一つだけ)。そして、玉を一斉に右隣へ移す。すでに右隣に玉 がある場合は動くことが出来ない(図 3.5)。ルールはこれだけである。箱に 玉は一つというルールを排除体積効果といい、ASEPはマクロ的で排除体積効果 を考慮した最も単純なモデルである。
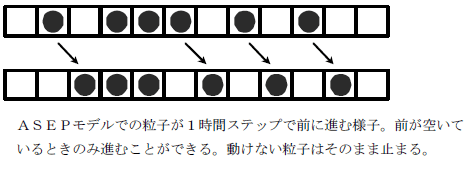
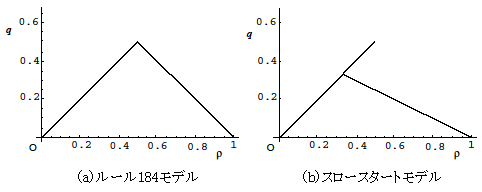
玉数が少ないと渋滞は発生しない。 一方、多いと互いが邪魔で動けない玉が発生する。 ASEP における密度の定義は、玉の数を箱の全数で割ったものとする。 したがって 184 モデルの臨界密度は 0.5 である(図 3.6)。 また、玉の数がちょうど箱の数の半分である臨界状態のときは、玉のある箱と ない箱が交互に出現する状態に落ち着く。
しかし、このモデルの渋滞相転移は極めて単純で、残念ながら高速道路のデー タに見られる複雑な現象を再現することが出来ない。 よって、この 184 モデルを拡張するためにルールを追加して現実の交通流に 近づけていく。 この研究では、前節で述べた基本図の逆ラムダ型(特に相転移時の頂点部)の 再現を目標として様々なルールが考えられてきた。 1 時間ステップあたりに進むセル数を増やす FI モデル、先行者だけでなくそ の先の車両を見通して早く移動するクイックスタートモデル、移動時にランダ ム性を考慮した NS モデル、超離散化の方法を使った新しいセルオートマトン モデルの BCA モデルなどであるが、実際に逆ラムダ型を再現できたのは次に 説明するスロースタートルールのみである。
スロースタート ルールは車の慣性の効果を入れたもので、一度止まった車は 動きにくいことを考慮したモデルである。 代表的なものとして、一度停止した車は前が空いて動けるようになっても一度 待ってから動き始める、とする一回休みのルールである。 停止した車以外はルール 184 モデルと同じである。 このルールを組み込むことで逆ラムダ型の枝を出すことが出来る(図 3.6)。 しかし、適当な乱数で初期条件を選んだだけでは出現せず、うまく初期条件を 設定しなけれならない。
このように ASEP は、マクロ的に交通流を再現した最も単純なモデルであるが 、現実のモデルとずれがあり、このようなルール作成とその詳細な数学的性質 を研究している段階である。
本研究では、StarLogo を使用した交通渋滞のシミュレーションを行う。 手法的には ASEP モデルに近い。 車一台一台をタートルとしてモデル化して、車の群による渋滞を再現するもの である。 ただし、StarLogo ではタートルはある程度連続的に動けるため、加速、減速 など速度や加速度を与えることができる。
本研究では簡単のために単車線の高速道路を仮定する。 この仮定の基では、車は衝突しないように制限速度を守りながら同一方向に移 動すればよい。 よって、個々の車両のルールは次の 3 つとなり、これはこれ以上簡単に出来な い最低限のルールである。
はじめに、車同士がどのような車間距離を保てば良いかを考える。
実際の交通流においてこの車間距離は、速度に応じて変化する。
速度が速いときは長く、遅いときは短い。
これは車の停止距離に等しいとされており、教習所ではこの停止距離を目安に
するよう教わる。
停止距離は、危険を発見してからブレーキを踏むまでの空走距離と、ブレーキ
を踏んでから実際に車が停止するまでの制動距離(brake distance;
直線上を一定の加速度で進む物体の運動を等加速度直線運動といい、初速度
また、式(4.1)より
減速度を
しかし、これらは連続時間における式であるので、StarLogo でモデル化する
ために離散時間で求める。
一定の加速度を時間ステップごとに加算するものとし、その連続加算回数を
また、加速度
また同じく、式(4.5)より
これより、離散時間における初速度
車は常にこの制動距離
さて、連続時間と離散時間の制動距離の誤差についてであるが、式(4.4)と
式(4.8)より、誤差は
次に加速時における条件を考える。
実際の運転において、車間距離が制動距離より長くなったからといって、すぐ
に加速するようなことはない。
アクセルを踏んでも、すぐにブレーキを踏まなくてはならないときがあるからで
、アクセル、ブレーキを頻繁に踏みかえるような人はいない。
よって、加速も減速も行わない先行車両に追従する車間距離の範囲が存在する
ものとし、これを追従車間距離(follow distance;
これらのことより、具体的な車の動きは次のようになり、これを繰り返すこと で交通流を再現する。
これを StarLogo のプログラミングで実現する。 タートルは次の処理を繰り返すことでモデルを実現する。
01:to drive
02: set D ( distance xcor-of ahcar ycor-of ahcar ) - l
03: set Db ( v * ( v + b ) ) / ( 2 * b )
04: set Da v + (( a * Pf * ( Pf + 1 )) / 2 ) +
(( v + a * Pf ) * ( v + a * Pf + b ) / ( 2 * b ))
05: ifelse D < Db[ set v v - b ][ if D > Da[ set v v + a ] ]
06: if v < 0[ set v 0 ]
07: if v > vlim[ set v vlim ]
08: forward v
09: set g g - 1
10: wait-until[ g < 1 ]
11: set g g + 1
12:end
各変数の意味は次の通りである。
グローバル変数
タートル変数
2-4 行目で車間距離、制動距離、加速車間距離を求める。
5行目で距離の判別を行い速度の値を加減する。
6、7 行目で、速度が 0 以上、制限速度以下にになるようにして、8 行目で、
設定した速度で前方に移動する。
9-11 行目で同期処理を行う。
StarLogo では厳密に並列処理を行うので、例えば加速可能か比較を行ったタ
ートルと、減速だけを行ったタートルでは、処理を抜けるタイミングが違う。
モデルでは加減速の判断、実行の時間単位を同一にしなければならないので、
wait-until 処理を使って同期処理を行っている。
変数 g には、あらかじめ車数(
このように StarLogo を使えば、交通流のモデルがわずか 10 行程度で実現可 能である。
作成したモデルが現実の観測事実と対応しているか検証する。 前節で作成したプログラムを元に、交通流の基本的な値を取れるように工夫し たものを作成した。 任意の密度、加速度、減速度を設定でき、車両を等間隔に配置して加速させて 、そのときの速度と流量を測定する機能を加えてある。 ソースコードを付録 A 、起動画面を図 4.1 にそれぞれ示す。
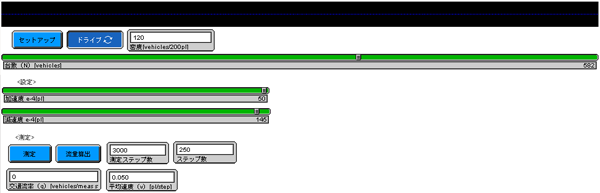
プログラム中の各変数の意味を次に示す。 なお、StarLogo における 1 パッチ分の長さを 1[pl]とする。
グローバル変数
タートル変数
スライダ変数
このシミュレーションを用いて、
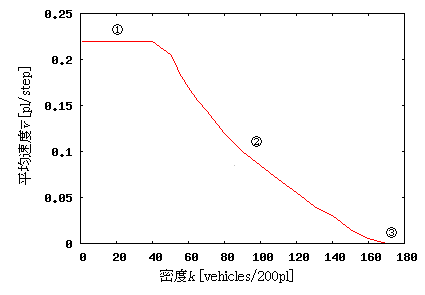
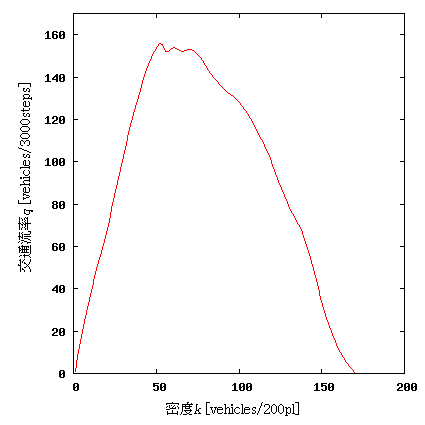
結果は、3 章で示した実測値と近い特性を示した。
本モデルは、StarLogo を用いて、車の動きをタートルにさせることにより交 通をシミュレートした。 車の動きが単純なのでタートルへ与えるプログラムも細かく、ほぼ車の動きの ルールの量にプログラムのステップ数が対応する。 このような単純なプログラムによるシミュレーションであるが、現実の観測値 と対応するところが多い。 これはこのモデルが渋滞の分析に適していることを示している。
また多くの交通流モデルは、渋滞流相において同じ密度で交通量を複数に安定 させることを目標としている。 本モデルでは、追従車間距離という考え方を取り入れることで、多重安定性を もたせることを試みた。 シミュレーションではその結果を測定することが出来なかったが、加減速をし ない車間距離の範囲を設けることで、同じ密度でも異なる交通量で安定させら れることは想像できる。 密度が増減しても、それによって増減した車間距離が追従車間距離の範囲内で あれば、車は加減速を行わない。 すなわち、密度増加によって速度を落としたあと、また元の密度に戻ったとし ても加速しないときがある。 よって、同じ密度でも違う速度で安定し、交通量が複数に安定する。 これは、シミュレーションで粗密波を発生させるなどのランダム性を取り入れ ることで、観測することができると思われる。 今回のシミュレーションでは、測定にランダム性を取り入れていない。 全車両は、速度 0 から等間隔で一定に同じタイミングで加速している。 よって、あるパラメータによってとりうる交通流率はただ一つであった。
本研究では自動車交通流のモデル化を行った。 StarLogo という無数にタートルを持てる処理系において、各タートルに車の 運転ルールを与えた。 モデルの調整は、車の運転ルールの変更なので容易に行える。 その結果、従来の研究に比べてプログラム量や解析にかかるトータルの時間は 少なく、その上で、実測値に近い結果が得られ、この手法の有用性が示された。
個々に単純な動作を行う個体群という枠組みは日常さまざまなところで遭遇す る。 このような個体群の振る舞いに関して StarLogo によるシミュレーションは非 常に有用であると思われる。
今回の研究では一車線道路の渋滞のみを扱ったが、今後はより複雑なモデルへ の適用も考えたい。
StarLogo ファイル
trafficjam8.0.slogo
`turtle`
to drive
if ms = true[
set xcs Xcor
sync
if who = 0[
set ms false
]
]
set D ( distance xcor-of ahcar ycor-of ahcar ) - l
set Db ( v * ( v + b ) ) / ( 2 * b )
set Da v + (( a * Pl * ( Pl + 1 )) / 2 )
+ (( v + a * Pl ) * ( v + a * Pl + b ) / ( 2 * b ))
ifelse D < Db[
set color red
set vtmp vtmp - b
][
ifelse D > Da[
set color yellow
set vtmp vtmp + a
][
set color blue
]
]
if vtmp > vlim[ set vtmp vlim ]
if vtmp < 0[ set vtmp 0 ]
set v vtmp
forward v
if who = 0[ set stepc stepc + 1 ]
sync
if me = true[
set xce Xcor
if who = 0[ set me false ]
]
end
to sync
set g g - 1
wait-until[ g < 1 ]
set g g + 1
end
to calcflow
let [ :xcsz xcs-of 0 ]
set q 0
if who = 0[ set q q + 1 ]
if xcs < :xcsz and :xcsz < xce[ set q q + 1 ]
if :xcsz < xce and xce < xcs[ set q q + 1 ]
if xce < xcs and xcs < :xcsz[ set q q + 1 ]
end
`observer`
globals[ a b S l Os k q stepc Pl vlim g mt ms me ]
turtles-own[ v vtmp ahcar D Db Da xcs xce ]
to setup
clear-all
set S screen-width
set l 0.4
set a as / 10000
set b bs / 10000
set Pl 15
set vlim 0.22
set ms false
set me false
set mt 3000
set stepc 0
create-turtles-and-do N[
ifelse who = 0[ set ahcar N - 1 ][ set ahcar who - 1 ]
set Heading 90
set color blue
set Xcor 0
set Ycor 0
set v 0
set vtmp 0
forward -1 * who * S / N
]
set g count-turtles
set k count-turtles-with [ (distance l / 2 0) <= 100 ]
end
to measure
set ms true
set stepc 0
wait-until[ stepc > mt ]
set me true
end| 1 | 0.220 | 1 |
| 9 | 0.220 | 33 |
| 20 | 0.220 | 67 |
| 29 | 0.220 | 99 |
| 40 | 0.220 | 133 |
| 50 | 0.205 | 154 |
| 53 | 0.195 | 156 |
| 54 | 0.190 | 155 |
| 55 | 0.185 | 153 |
| 60 | 0.170 | 154 |
| 65 | 0.155 | 152 |
| 70 | 0.145 | 153 |
| 80 | 0.120 | 145 |
| 90 | 0.100 | 135 |
| 100 | 0.085 | 128 |
| 110 | 0.070 | 116 |
| 120 | 0.055 | 99 |
| 130 | 0.040 | 79 |
| 140 | 0.030 | 63 |
| 150 | 0.015 | 34 |
| 160 | 0.005 | 12 |
| 170 | 0 | 0 |