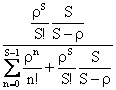 �ɂȂ�A�v�Z������ł���B
�ɂȂ�A�v�Z������ł���B�@�҂��s�_�Ƃ������̂�����B������g���ƁA�Ⴆ��s��ATM�̏��Ԃ�҂��Ă���҂��s��ɂ��āA���ω����҂�����邩�A�s��ő҂��Ă���l���͕��ω��l���Ȃǂ��v�Z���邱�Ƃ��ł���B���̍ۂɁA�P�ʎ��ԓ�����ɗ��镽�ϐl���i�Ɂj�A�P�ʎ��ԓ�����ɋA�镽�ϐl���i�Ɂj�Ȃǂ̃p�����[�^���K�v�ɂȂ�B
�@�҂��s�_�́A�d�b��ЂɋΖ����Ă����A�[�����Ƃ����l�����A�u���e�����d�b�T�[�r�X����邽�߂ɁA�ǂꂾ���̉����p�ӂ���K�v�����邩�v�����肷�������ꂽ���Ƃ����������ɂ���ꂽ�B�҂��s�_�̒��ɃA�[����C���Ƃ������̂�����B����́A�Ⴆ�R�[���Z���^�[�ɂ�����ꂽ�d�b�������Ɍq����Ȃ��m�����v�Z������̂ŁA�I�y���[�^�̐l����S�l�A���p���ρi���Ɂ^�ʁj�Ƃ���ƁA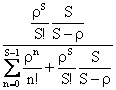 �ɂȂ�A�v�Z������ł���B
�ɂȂ�A�v�Z������ł���B
�@�C���^�[�l�b�g�̉�͂̂��߂ɊJ�����ꂽNS2�Ƃ����\�t�g�E�F�A������BNS2�ł́A�\���������l�b�g���[�N��Object Tcl����ŋL�q����ƁA���̃l�b�g���[�N�̃g���t�B�b�N���V�~�����[�V�����ł���\�t�g�E�F�A�ł���B
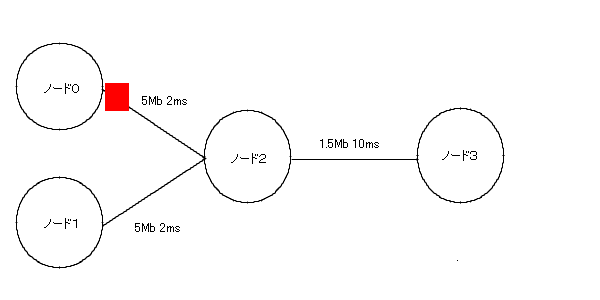
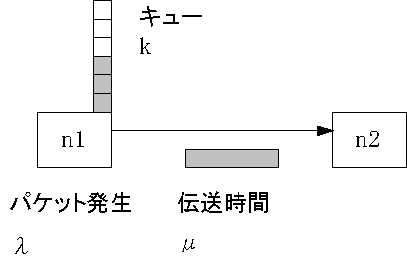
�@�g�p��Ƃ��ẮA�}�P�̂悤�Ƀm�[�h�A�m�[�h�Ԃ̃����N�i������x�A�x���j�A�v���g�R���Ȃǂ�ݒ肵�āA�p�P�b�g�𑗂�v���O����������B
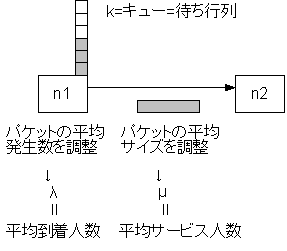
�}�Q�̂悤�ȃv���O����������ANS�Q�ő҂��s�f�����V�~�����[�V��������B
�@�{�����ł́A�v�Z������ȑ҂��s�_�̎������ۂɌv�Z�����A����ɃV�~�����[�V�������ʂ��瓚�����Ȃ����ׂ�B��̓I�ɂ́A�҂��s�f��M/M/1(k)�̌đ��������߂�A�[����B���A�҂��������߂�A�[����C���̕��͂����āA���_�l�Ǝ����l�̔�r������B
�@��Q�͂ł́A�҂��s�_�̐����ƃA�[����B���E�A�[����C���̓��o���s���B��R�͂ł́A���͂Ɏg�p�����\�t�g�E�F�A�̐��������Ă���B��S�͂ł́A�V�~�����[�V�����������s���B��T�͂ł͂܂Ƃ߂��s���Ă���B
�@�҂��s�_�́A�ʐM�g���q�b�N���_�Ǝ��Ă���A���݂͓����������B�p��͈قȂ邪�A�����ȗ��_�Ǝv���ėǂ��B
�@�ʐM�g���q�b�N���_�́A�d�b�ʐM�Ԃ̌����ݔ��̉�́E�v�̂��߂̗��_�ŁA�Q�O���I�̎n�߂Ƀf���}�[�N��A.K.Erlang�i�A�[�����j�ɂ���Ă���ꂽ�B
�@����A�T�[�r�X������ŏd�v�Ȏ��_�Ƃ��āA���[�U�W�c���甭�����Ă�����v�̗ʂƁA���̎��v���~�߂ăT�[�r�X�������i�ݔ���l�j�A�����Ă��̌��ʂƂ��Č����T�[�r�X�i����\������B�҂��s�_�͂��̎O�̊W�Ɋm���_��p���Đ��w�I�ȍ�����^���闝�_�ł���B
�@�҂��s�_�́A����E��풆�ɕĉp�R�ɂ��J�����ꂽ�I�y���[�V�����Y���T�[�`�i���w�I�ȃA�v���[�`�ɂ��o�c���̈ӎv������x������j�̕���ɂ����Č�������A�������A��ʖ��A�ɊǗ����̍L������ɓK�p����Ă���B
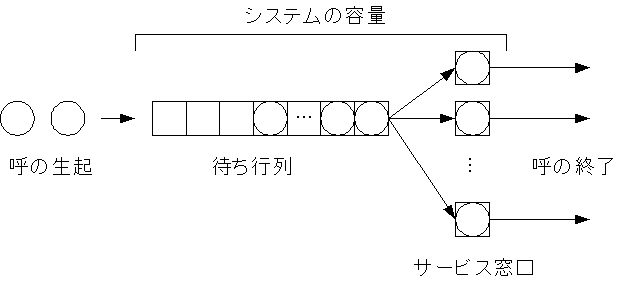
�@�҂��s��̃��f���ł́A�q�����đ����ɕ��сA���Ԃ�����Α����ŃT�[�r�X���A�T�[�r�X���I���q�͋���A�Ƃ������̂ł���B�҂��s�_�ƒʐM�g���q�b�N���_�Ŏg����p��͈Ⴄ�̂ŁA�Ή��\��\�P�Ɏ����B
�\�P�D�҂��s�_�ƒʐM�g���q�b�N���_�̗p��̑Ή��\
| �҂��s�_ | �q | �T�[�r�X | ���� |
| �ʐM�g���q�b�N���_ | �āi�d�b��f�[�^�Ȃǂ̐ڑ��v���j | �ۗ� | �o�� |
�@�҂��s��V�X�e���́A���̌܂̗v�f����Ȃ�m�����f���ŕ\�����B
�@�������Aa�^b�^c�id�j�ƕ\�L����̂��P���h�[���̋L���ƌĂ��B�A���A����a�Ab�Ac�Ad�Ae�Ƃ��Ĉȉ��̂悤�ȕ\�L���p������B
�@a��b�́A�m�����z�ł���A�ȉ��̋L���̂����ꂩ�ŕ\����邱�Ƃ�����B
�@c�͎��R���ł���B�T�[�r�X�����̐�����������A��x�ɕ����̌Ă��������Ƃ��\�ɂȂ�A�����������オ��B
�@d�̑҂��s��̒����̏�������R���ł���B����́A�҂��s��ɓ��邱�Ƃ��ł���Ă̍ő�l�ł���B�҂��s��̒����̏�����L���̏ꍇ�͂��܂���S�ƕ\�L���A�����̏ꍇ�͏ȗ������B�҂��s��ɋ��������ɌĂ���������ƁA���̌Ă͎̂Ă���B
�@e�̏����K�͂́A�ʏ퓞�������Ă��珈�������铞���������iFIFO�FFirst In First Out�j�ŁA���ɕ\�L����邱�Ƃ͖����B���ɂ��A�t�������iLIFO�j�A�����_�������Ȃǂ�����B
�@���ɁA�{�����ň����҂��s�f��M/M/1(k)�́A�Ă̓������ԊԊu�ƕۗ����Ԃ��w�����z�ɂ���ă����_���Ɍ��܂�A�T�[�r�X�����̐��͈�A�V�X�e���̗e�ʂ͂��ł���Ƃ����Ӗ��ł���B
�@�Ă������_���ɔ�������ߒ�����͂���B�����_���ȌĂ̔����́A���̃��[���ɏ]���Ƃ���B
��̎O�̃��[���̂��ƂɁA����(0,t)���ɂ��̌Ă����N����m��![]() �����߂�B����(0,t)���\�������̂��̋�Ԃɕ������A��̋�Ԃ��������
�����߂�B����(0,t)���\�������̂��̋�Ԃɕ������A��̋�Ԃ��������![]() �Ƃ���B�����ŁA�P�ʎ��Ԓ��ɌĂ����������m���N���Ƃ�
�Ƃ���B�����ŁA�P�ʎ��Ԓ��ɌĂ����������m���N���Ƃ�![]() �ŕ\���B���̋�Ԃ̂����A����̂��̋�ԂŌĂ��������A�c���(n-k)�̋�ԂŔ������Ȃ��m����
�ŕ\���B���̋�Ԃ̂����A����̂��̋�ԂŌĂ��������A�c���(n-k)�̋�ԂŔ������Ȃ��m����
![]() �ƂȂ�B���̋�Ԃ̑I�ѕ���
�ƂȂ�B���̋�Ԃ̑I�ѕ���
![]() �ʂ肠�邱�Ƃ��l�����A
�ʂ肠�邱�Ƃ��l�����A
![]() �A
�A![]() �Ƃ���ƁA
�Ƃ���ƁA
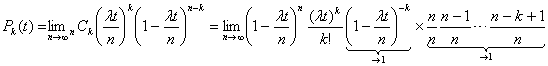
�l�C�s�A���̒�`��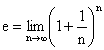 �𗘗p����ƁA�ŏI�I��
�𗘗p����ƁA�ŏI�I��
![]()
����́A���ϒl![]() �̃|�A�\�����z�ł���B���̂悤�Ȑ��N���|�A�\�����N�ƌĂԁB
�̃|�A�\�����z�ł���B���̂悤�Ȑ��N���|�A�\�����N�ƌĂԁB
����(0,t)���Ɉ���Ă��������Ȃ��m����![]() �ƂȂ�B���������āA(0,t)�ȓ��ɌĂ���������m���́A
�ƂȂ�B���������āA(0,t)�ȓ��ɌĂ���������m���́A![]() �ɂȂ�̂ŁA�Ă̐��N�Ԋu�̕��z����
�ɂȂ�̂ŁA�Ă̐��N�Ԋu�̕��z����
![]()
�ƂȂ�A���ϒl![]() �̎w�����z�ɏ]���B���̂悤�ɁA���N�Ԋu���w�����z�ƂȂ邱�Ƃ��A�����_�����N�̓����ł���B
�̎w�����z�ɏ]���B���̂悤�ɁA���N�Ԋu���w�����z�ƂȂ邱�Ƃ��A�����_�����N�̓����ł���B
�@�Ă������_���ɏI������i�ۗ����Ԃ��I���j�ꍇ�ɂ��čl����B����́A��������![]() ���ɌĂ��I������m�����A�����ɖ��W��
���ɌĂ��I������m�����A�����ɖ��W��![]() �ƂȂ郂�f���ɑ�������B�i
�ƂȂ郂�f���ɑ�������B�i![]() �F�I�����j
�F�I�����j
�@�ۗ����Ԃ������傫���Ȃ�m���́A���Ԃ����ɌĂ��I�����Ȃ��m���Ɠ������B�����ŁA���Ԃ������̔������
l![]() �ɕ�������A���Ԃ����ɌĂ��I�����Ȃ��m����
�ɕ�������A���Ԃ����ɌĂ��I�����Ȃ��m����
![]() �ƂȂ邩��A
�ƂȂ邩��A
![]() �A
�A
![]() �Ƃ���ƁA�ۗ����Ԃ�������m����
�Ƃ���ƁA�ۗ����Ԃ�������m����
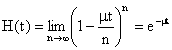
�ƂȂ�B���Ȃ킿�A�ۗ����Ԃ������Ȃ��m���͕��ϒl![]() �̎w�����z�ɏ]���B
�̎w�����z�ɏ]���B
�@�{�����ň����҂��s�f��M/M/1(k)�̉�͂��s���B�Ă̓������z�����N���ɂ̃|�A�\�����z�A�ۗ����ԕ��z���I�����ʂ̎w�����z�A�T�[�r�X�����̐����P�A�҂��s��̒����̏����
k�ł���B�����ŁA���p��![]() ���`����B����́A�T�[�r�X�����ŒP�ʎ��ԂɏI������Ă̐��ɑ��āA�P�ʎ��ԓ�����A���{�̌Ă��������邩��\���Ă���B�P�ʂƂ��ẮA
[erl]�i�A�[�����j��p����B�V�X�e���̗e�ʂ������̃V�X�e���ł́A�Ɂ��ʁi�ρ��P�j�Ȃ�ΌĂ̔�������X�s�[�h���Ă̏I������X�s�[�h�����邱�ƂɂȂ�A
�҂��s��̒����͂ǂ�ǂ��Ȃ��Ă��܂��B���������āA�V�~�����[�V�������I���Ȃ��Ȃ��Ă��܂��̂Œ��ӂ��K�v�ł���B����A�V�X�e���̗e�ʂ��L���Ȃ�A���ӂꂽ���͎̂Ă���B
���`����B����́A�T�[�r�X�����ŒP�ʎ��ԂɏI������Ă̐��ɑ��āA�P�ʎ��ԓ�����A���{�̌Ă��������邩��\���Ă���B�P�ʂƂ��ẮA
[erl]�i�A�[�����j��p����B�V�X�e���̗e�ʂ������̃V�X�e���ł́A�Ɂ��ʁi�ρ��P�j�Ȃ�ΌĂ̔�������X�s�[�h���Ă̏I������X�s�[�h�����邱�ƂɂȂ�A
�҂��s��̒����͂ǂ�ǂ��Ȃ��Ă��܂��B���������āA�V�~�����[�V�������I���Ȃ��Ȃ��Ă��܂��̂Œ��ӂ��K�v�ł���B����A�V�X�e���̗e�ʂ��L���Ȃ�A���ӂꂽ���͎̂Ă���B
�@�V�X�e�����Đ��́A�O�A�P�A�`�ik-�P�j�Ak�̂����ꂩ�ł���B���ꂼ��̏�ԂɑΉ��������m���i�������܂ŐL���ƁA�Ɍ��l�ɂȂ�j���A
![]() �Ƃ���B������A��ԑJ�ڐ}�ŕ\���ƁA
�Ƃ���B������A��ԑJ�ڐ}�ŕ\���ƁA
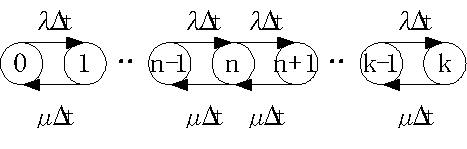
�̂悤�ɂȂ�B
�@��ԑJ�ڐ}�̒��ɂ�����́A�m���I�ȗ���̏o�����\���Ă���B���Ƃ��A�in-�P�j��
n�̊Ԃ̏�ɂ�����́A�������̎��ɃV�X�e�����Đ���n-1�ŁA![]() ��ɃV�X�e�����Đ���n�ɂȂ�m���́A
��ɃV�X�e�����Đ���n�ɂȂ�m���́A![]() �ƂȂ�B�Ȍ�A
�ƂȂ�B�Ȍ�A![]() �͏ȗ����ċL�q����B�אڂ���V�X�e�����Đ��̊Ԃ̊m���I�ȗ���̏o���肪������
(Flow-out=Flow-in)�Ƃ�������������̂ŁA
�͏ȗ����ċL�q����B�אڂ���V�X�e�����Đ��̊Ԃ̊m���I�ȗ���̏o���肪������
(Flow-out=Flow-in)�Ƃ�������������̂ŁA
![]()
![]()
�Ƃ�����������B�����ƁA���ׂĂ�Pn�̘a���P�Ƃ����W
![]()
�����m��Pn���v�Z���邱�Ƃ��ł���B
���i�P�j���A![]() �ł���B
�ł���B
���i�R�j�ɂ�����n=1�Ƃ��āA����Ɏ��i�T�j��������ƁA
![]()
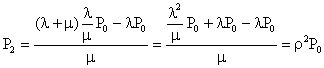
����ɁA![]() �����߂�ƁA
�����߂�ƁA
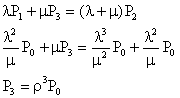
�ƂȂ�̂ŁA���l�ɂ���
![]()
�ƂȂ�B���i�U�j���A![]() �����i�Q�j�ɑ������ƁA
�����i�Q�j�ɑ������ƁA
![]() �ƂȂ�B���ǁA���ׂĂ�
�ƂȂ�B���ǁA���ׂĂ�
n=0,1,2,�c,k�ɑ���
![]()
�ƂȂ�B���i�V�j�����i�S�j�ɑ������
![]()
�ƂȂ�B���䋉���̘a�̌������![]() �ƂȂ�̂ŁA���i�W�j���A
�ƂȂ�̂ŁA���i�W�j���A
![]()
�ƂȂ�A���������āA���i�V�j���
![]()
��B
�@�A�[����B���́A���������Ă��V�X�e���ɋ������̂Ŏ̂Ă��Ă��܂��m���A�đ������v�Z���鎮�ł���B
�@�A�[����B�������߂ɁA�҂��s�f��M/M/S(0)�̉�͂��s���B�Ă̓������z�����N���ɂ̃|�A�\�����z�A�ۗ����ԕ��z���I�����ʂ̎w�����z�A�T�[�r�X�����̐���S�ł���B���̃��f���ł͑҂��s��͖����B�V�X�e�����Đ���S�̂Ƃ��̒��m�����A�A�[����B���ł���B
�@�V�X�e�����Đ��́A�O�A�P�A�`�iS-�P�j�AS�̂����ꂩ�ł���B���ꂼ��̏�ԂɑΉ��������m�����A
![]() �Ƃ���B������A��ԑJ�ڐ}�ŕ\���ƁA
�Ƃ���B������A��ԑJ�ڐ}�ŕ\���ƁA
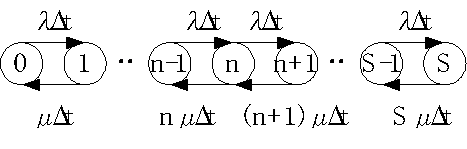
�@���̏�ԑJ�ڐ}�ɂ��A
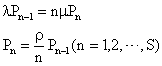
��B�����ό`���āA
![]()
![]() �̓V�X�e���ɌĂ��Ȃ���Ԃ̊m���ŁA���K������
�̓V�X�e���ɌĂ��Ȃ���Ԃ̊m���ŁA���K������
![]() ���
���
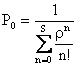
�ƌ��肳���B��������
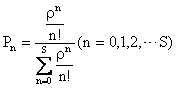
�ƂȂ邱�Ƃ������ꂽ�B���̎�����V�X�e�����Đ���S�̒��m�������߂��

���ꂪ�AM/M/S(0)�^�̃A�[����B���ł���B
M/M/1(k)�^�ł́A�U�y�[�W�̎��i�X�j�����m����![]() �ŕ\�����̂ŁA�A�[����B���́A
�ŕ\�����̂ŁA�A�[����B���́A
![]()
�ɂȂ�B
�@�A�[����C���́A���������Ă��҂��s��ő҂������m���A�҂������v�Z���鎮�ł���B
�@�A�[����C�������߂ɁA�҂��s�f��M/M/S�̉�͂��s���B�Ă̓������z�����N���ɂ̃|�A�\�����z�A�ۗ����ԕ��z���I�����ʂ̎w�����z�A�T�[�r�X�����̐���S�A�V�X�e���̗e�ʂ͖����ł���B���̃��f���̒P�ʎ��ԓ�����̏I������Ă̐���S�ʌȂ̂ŁA�Ɂ�S�ʂ������ł���B�T�[�r�X�����ɋ������A�܂�A�V�X�e�����Đ���S�ȏ�̒��m���̘a���A�[����C���ł���B
�@�V�X�e�����Đ��́A�O�A�P�A�`�iS-�P�j�AS�A�c�ł���B���ꂼ��̏�ԂɑΉ��������m�����A![]() �Ƃ���B�����ŁA�T�[�r�X�����ɋ�����ꍇ(a)�i����S�j�ƁA�T�[�r�X�����ɋ������ꍇ(b)�i����S�j�ɕ����čl���Ă݂�B������A��ԑJ�ڐ}�ŕ\���ƁA
�Ƃ���B�����ŁA�T�[�r�X�����ɋ�����ꍇ(a)�i����S�j�ƁA�T�[�r�X�����ɋ������ꍇ(b)�i����S�j�ɕ����čl���Ă݂�B������A��ԑJ�ڐ}�ŕ\���ƁA
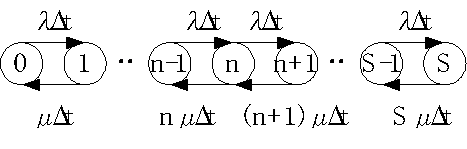
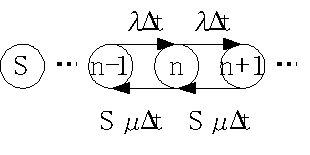
�@(a)�̏ꍇ�́A�A�[�����a���̂Ƃ��Ɠ��l�ɁA
![]()
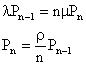
![]()
�@(b)�̏ꍇ�́A
![]()
�����藧�B�����ŁA���i�P�O�j�ɂ����r�|�P�������āA
![]()
�ƂȂ�B���i�P�P�j����A![]() ��m���āA���i�P�R�j�ɑ������ƁA
��m���āA���i�P�R�j�ɑ������ƁA
![]()
���i�P�Q�j�ɂ���S�������āA
![]()
���i�P�Q�j�ɂ���S�{�P�������āA
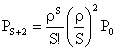
���l�ɂ��āA
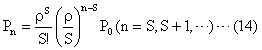
��B����ŁA���ׂĂ̂��ɑ��āA![]() ��
��![]() �ŕ\�����Ƃ��ł����̂ŁA�Ō�ɐ��K������
�ŕ\�����Ƃ��ł����̂ŁA�Ō�ɐ��K������![]() ���
���![]() �̒l���v�Z���邱�Ƃ��ł���B���i�P�P�j�Ǝ��i�P�S�j���
�̒l���v�Z���邱�Ƃ��ł���B���i�P�P�j�Ǝ��i�P�S�j���
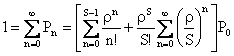
�܂��A�ρ�S�̂Ƃ��ɂ��̖��������͎�������̂ŁA
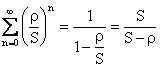
�ƂȂ�A�ŏI�I��
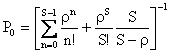
![]() ���킩�������Ƃɂ��A���ׂĂ̂��ɑ���
���킩�������Ƃɂ��A���ׂĂ̂��ɑ���
![]() ���킩��悤�ɂȂ����B
���킩��悤�ɂȂ����B
���������āA�A�[����C���̓V�X�e�����Đ���S�ȏ�̒��m���̘a�Ȃ̂ŁA
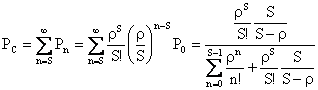
�ɂȂ�B
M/M/1(k)�^�̃A�[����C���́A�V�X�e�����Đ�����ȏ�̎��̒��m��![]() �i�U�y�[�W�̎��i�X�j���j�̘a�Ȃ̂ŁA
�i�U�y�[�W�̎��i�X�j���j�̘a�Ȃ̂ŁA
![]()
�ƂȂ�B�܂��A���K������![]() ���A
���A
![]()
�ł��悢�B
�@NS2�Ƃ́C�J���t�H���j�A��w�o�[�N���C�Z�ŊJ�����ꂽ�l�b�g���[�N�V�~�����[�^�ł���BNS2�̃\�[�X�C�}�j���A���C�p��̃`���[�g���A���Ȃǂ�http://www.isi.edu/nsnam/�Ŏ擾�ł���BNS2�́AC++��OTcl�ŏ����ꂽ�I�u�W�F�N�g�w���̃C�x���g�h���u���E�l�b�g���[�N�V�~�����[�^�ł���BNS2���̂�C++�ŋL�q����Ă���A�C���^�[�t�F�[�X�̑����OTcl�ōs���B
�@�ȒP�Ȏg�p���������ƁA�܂��A�m�[�h�ƃ����N������A�����N�̍ō��]�����x�Ȃǂ̃p�����[�^�����߁A�m�[�h�Ԃłǂ̂悤�ȒʐM�i�p�P�b�g�T�C�Y��ڑ��`���j���s���������߂Ă���V�~�����[�g���J�n����A�e�L�X�g�G�f�B�^�Ō��邱�Ƃ��ł���o�̓t�@�C����������B���̏o�̓t�@�C���ɂ́A�}�C�N���Z�J���h�P�ʂŃp�P�b�g�̓������ڍׂɋL�^����Ă���B
�@Otcl�̍\�����������B��{�I�ɂ́u�R�}���h�@�����P�@�����Q�@�c�v�Ƃ����`�ł���B��Ԏg����R�}���h��set�̎g�p��́uset a 1�v�ȂǁB�ϐ�a��1�Ƃ����l��������B�ϐ��ɂ͕�����␔���Ȃǂ̌^�͖����B
�@�ϐ��̒l���g�������Ƃ��́A�ϐ��̑O��$������B��̓I�ɂ́A�uset b a�v�Ə����Εϐ�b�̒l��a�ɂȂ邪�A�uset b $a�v�Ə����Εϐ�b�̒l��1�ɂȂ�B
�@�v�Z�����������́A�uset c [expr 1+1]�v�Ƃ����悤�ɏ����A�ϐ�c�̒l�͌v�Z���ʂ�2�ɂȂ�B����́A�܂�expr�R�}���h��1+1���v�Z���A���̌��ʂ�[ ]�����̒l��Ԃ��������̖��������Ă��邽�߂ł���B
�@�I�u�W�F�N�g������ɂ́A�uset �I�u�W�F�N�g�̖��O [new �I�u�W�F�N�g�̎��]�v�Ə����܂��B���������I�u�W�F�N�g�ɖ��߂��o�������Ƃ��́A�u$�I�u�W�F�N�g�̖��O �R�}���h �����v�Ə����܂��B
�@���[�U�[�Ǝ��̊�����肽���ꍇ�́A�uproc ���̖��O �o�����p�o���e�p�v�Œ�`����B���̊��̒��̕ϐ��͊�{�I�Ƀ��[�J���ϐ��Ȃ̂ŁAglobal�錾�����ăO���[�o���ϐ��ɂ���K�v������B
�@Perl�́AWeb�y�[�W�̌f����`���b�g�Ȃǂ�CGI��V�X�e���Ǘ��A�e�L�X�g�����Ȃǂ̃v���O�����Ɏg����C���^�v���^�����̃v���O���~���O����ŁALarry Wall���ɂ���ĊJ������A1987�N�Ɉ�ʌ��J���ꂽ�B�L�q�̔������������p�������b�g�[�ɂ��Ă���B������UNIX��ŗ��p���ꂽ���A���݂ł̓{�����e�B�A�ɂ��Windows��Macintosh�Ȃǂ̃v���b�g�t�H�[���ɈڐA����A�}���ɕ��y�𐋂��Ă����BPerl�Ƃ������̂ɂ́A���̓�̃L�[���[�h�̈Ӗ�������B
�@Perl�̍\����C����Ɏ��Ă���A���͂ȕ����Z�@�\�����邽�߁A�{�����Ŏg�p�����B
�@�����̏������܂Ƃ߂čs���i�o�b�`�����j�Ƃ��Ɏg����AOS�̃V�F�������ډ��߁E�����ł���X�N���v�g�B�V�F���X�N���v�g�̓V�F�����ƂɓƎ��̋@�\���g�p���ď�������邽�߁A�N���̕��@�╶�@�̓V�F���ɂ���ĕς���Ă���B�Ⴆ��UNIX�nOS�i�����ɂ͂��̏�œ��삷��bash�Ȃǂ̃V�F���j�ł́A�V�F���ɃV�F���X�N���v�g�������Ƃ��ēn���Ď��s������A�V�F���X�N���v�g�̖`���ɋN���v���O��������������ŃV�F���X�N���v�g���̂����s�����肷��ƋN���ł���B�V�F���X�N���v�g�ł̓V�F�����ƂɓƎ��̕��@���̗p����Ă��邪�A�����ނˈ�s����̃R�}���h�Ƃ��Ĉ�����B����UNIX�nOS�̃V�F���͕��G�ȌJ��Ԃ��������������ȂǂɑΉ����Ă���A�V�F���X�N���v�g�����ł��Ȃ蕡�G�ȏ������������ł���B
�@cygwin�́AMicrosoftWindows�I�y���[�e�B���O�V�X�e����œ��삷��UNIX���C�N�Ȋ��̈�ł���B�����œ���E�g�p�ł���B�{�����Ŏg�p����NS2��UNIX�p�ɊJ�����ꂽ�\�t�g�E�F�A�Ȃ̂ŁAWindows�Ŏg�����߂�cygwin���g�p�����B
�@�҂��s�f��M/M/1(k)�̓��������V�~�����[�V���������邽�߂ɁA��̃m�[�h������B�����āA������瑼���ւƃp�P�b�g�𑗂葱����悤�ɂ���B���̍ہA�p�P�b�g�̔������鎞�ԊԊu���Ă̓������ԊԊu���z���f���A�p�P�b�g�̃f�[�^�T�C�Y��ۗ����ԕ��z���f���ɂ݂��Ă�i�p�P�b�g�̃f�[�^�T�C�Y�ɂ���āA�p�P�b�g���`���H��ʂ鎞�Ԃ��ς�邽�߁j�B�����āA���ꂼ����w�����z�ɂ���B�T�[�r�X��������ŁA�`���H�̃L���[���V�X�e���̗e�ʂɂ݂��Ă�B�����}�ɂ���Ɛ}�V�ɂȂ�A�v���O�����umm1k.tcl�v���ȉ��Ɏ����B
mm1k.tcl
set lambda [lindex $argv 0]
set mu [lindex $argv 1]
set qsize [lindex $argv 2]
set ns [new Simulator]
set tf [open out.tr w]
$ns trace-all $tf
set n1 [$ns node]
set n2 [$ns node]
set link [$ns simplex-link $n1 $n2 100kb 0ms DropTail]
$ns queue-limit $n1 $n2 $qsize
set InterArrivalTime [new RandomVariable/Exponential]
$InterArrivalTime set avg_ [expr 1/$lambda]
set pktSize [new RandomVariable/Exponential]
$pktSize set avg_ [expr 100000.0/(8*$mu)]
set src [new Agent/UDP]
$ns attach-agent $n1 $src
set qmon [$ns monitor-queue $n1 $n2 [open qm.out w] 0.1]
$link queue-sample-timeout
proc finish {} {
global ns tf
$ns flush-trace
close $tf
exit 0
}
proc sendpacket {} {
global ns src InterArrivalTime pktSize
set time [$ns now]
$ns at [expr $time + [$InterArrivalTime value]] "sendpacket"
set bytes [expr round ([$pktSize value])]
$src send $bytes
}
set sink [new Agent/Null]
$ns attach-agent $n2 $sink
$ns connect $src $sink
$ns at 0.0001 "sendpacket"
$ns at 1000.0 "finish"
$ns run
�v���O�����ł́A���N���Ɂi�p�P�b�g�����̎��ԊԊu�j�A�I�����ʁi�p�P�b�g�̃f�[�^�T�C�Y�j�A�V�X�e���̗e�ʁi�`���H�̃L���[�̃T�C�Y�j�A���v���O�����̎��s���ɃR�}���h���C����������Ƃ��Ď����Ă���悤�ɂ��Ă���B�����āA��̃m�[�h������A���̃m�[�h�Ԃ̓`���H�̓`�����x�A�L���[�̃T�C�Y�����߂�B�����āA�p�P�b�g�����̎��ԊԊu�ƃp�P�b�g�̃f�[�^�T�C�Y�̕��ϒl���w�����z�ɐݒ肷��i���̃v���O�����ł́A�`���H�̓`�����x�ƃp�P�b�g�̃f�[�^�T�C�Y�����܂��������āA�R�}���h���C�����玝���Ă������N���ƏI���������̂܂g����悤�ɂȂ��Ă���j�B��̃m�[�h�Ԃ̐ڑ��ɂ����āAUDP�iUser Datagram Protocol�F�p�P�b�g������ɓ͂��Ȃ��Ă��A�đ����Ȃ��Ƃ����ݒ�j�A�I�����̎葱���A�p�P�b�g���M�̐ݒ�����߂�B�Ō�ɁA�V�~�����[�V����������0.0001�b����J�n���A1000.0�b�ŏI������B
�@NS2�̃v���O���������s����ƁA�ȉ��̂悤�Ɂuout.tr�v�Ƃ����e�L�X�g�t�@�C�����ł���B
+ 681.616875 0 1 udp 109 ------- 0 0.0 1.0 21231 21231 + 681.628971 0 1 udp 25 ------- 0 0.0 1.0 21232 21232 d 681.628971 0 1 udp 25 ------- 0 0.0 1.0 21232 21232 r 681.648839 0 1 udp 965 ------- 0 0.0 1.0 21227 21227 - 681.648839 0 1 udp 24 ------- 0 0.0 1.0 21228 21228 r 681.650759 0 1 udp 24 ------- 0 0.0 1.0 21228 21228 - 681.650759 0 1 udp 234 ------- 0 0.0 1.0 21229 21229 + 681.662248 0 1 udp 437 ------- 0 0.0 1.0 21233 21233
�@��̍s�ɃX�y�[�X�ŋ��ꂽ�P�Q�̍��ڂ�����A��Ԗڂ��珇��
�@�l�̕���(r,+,-,d)�̂����ꂩ�ŕ\����A r:receive�@�p�P�b�g�̎�� +:enqueued�@�`���H�̃L���[�Ƀp�P�b�g������ -:dequeued�@�p�P�b�g���`���H�̃L���[����o�� d:drop�@�`���H�̃L���[�����^���ŁA�p�P�b�g���̂Ă� ���Ӗ�����B
�@��\���Ă���B���̂����A�����ɕK�v�Ȃ̂͂P�D�C�x���g�̎�ށA�Q�D�C�x���g�������������ԁA�P�Q�D�p�P�b�g�̘A���ԍ��ł���B�đ��������߂邽�߂ɂ́A���ꂽ�p�P�b�g�Ǝ̂Ă�ꂽ�p�P�b�g�𐔂��āA�đ������̂Ă�ꂽ�p�P�b�g�^�i���ꂽ�p�P�b�g�{�̂Ă�ꂽ�p�P�b�g�j�ŋ��߂邱�Ƃ��ł���B�҂����́A���������p�P�b�g�i�����ꂽ�p�P�b�g�{�̂Ă�ꂽ�p�P�b�g�j�ƃL���[�ő҂��Ȃ������p�P�b�g�i�L���[�ɓ����������Əo�������������j�𐔂��āA�҂������i���������p�P�b�g�|�҂��Ȃ������p�P�b�g�j�^���������p�P�b�g�ŋ��߂邱�Ƃ��ł���B�Ō�ɗ��p���A�đ����A�҂������o�͂���v���O�����umm1k.pl�v���ȉ��Ɏ����B
�@�v���O�������ł́A$n1�Ɂuout.tr�v�����s�ǂݍ��݁A�P�Q�̍��ڂ�@d1�Ƃ����z��Ɋi�[���Ă���B���̒��ł��A�K�v��$d1[0] �i�C�x���g�̎�ށj�A$d1[1] �i�C�x���g�������������ԁj�A$d1[11]�i�p�P�b�g�̘A���ԍ��j���g���B$receive�ɂ̓m�[�h�Q�Ŏ��ꂽ�p�P�b�g�̐����A$drop�ł͎̂Ă�ꂽ�p�P�b�g�̐����J�E���g���Ă���B@plus�ɂ͂��ꂼ��̃p�P�b�g���L���[�ɓ��������Ԃ��A@minus�ɂ̓L���[����o�����Ԃ��L�^���Ă���B$nowait�ɂ́A�L���[�ő҂�����Ȃ������p�P�b�g�̐����J�E���g���Ă���B�Ō�ɗ��p��$ro�A�đ���$koson�A�҂���$mati���o�͂���
mm1k.pl
open(IN, 'out.tr');
@temp = <IN>;
@plus;
@minus;
$receive=0;
$drop=0;
foreach $n1 (@temp){
chomp;
@d1 = split(/ /,$n1);
if($d1[0] eq '+'){
$plus[$d1[11]] = $d1[1];
}
elsif($d1[0] eq '-'){
$minus[$d1[11]] = $d1[1];
}
elsif($d1[0] eq 'r'){
$receive++;
}
elsif($d1[0] eq 'd'){
$drop++;
}
}
$i = 0;
$nowait = 0;
for ($i=0;$i<=$#minus;$i++){
if (defined($minus[$i])){
if ($minus[$i] == $plus[$i]){
$nowait++;
}
}
}
$koson=$dr/($dr+$re);
$mati=($drop+$receive-$nowait)/($drop+$receive);
$ro=$ARGV[0]/$ARGV[1];
print "$ro,$koson,$mati\n";
�@�A�[����B�EC���̃O���t��`�����߂ɁA����L���[�̐��ɑ��ė��p�����O�`�P�͈̔͂ŕω��������̂��K�v�ɂȂ�B������A�V�F���X�N���v�g�ɂ��J��Ԃ������ōs���B�v���O�����̎��s���ɁA�R�}���h���C������l�̈����i�J�n���̐��N���A�I�����̐��N���A�I�����A�L���[�̐��j����͂���B�I�����͌Œ�ŁA���N�����グ�Ă������Ƃɂ��A���p�����オ���Ă����A���ꂼ��̗��p���̎���NS2�̃v���O������Perl�̃v���O���������s���āA�đ����A�҂�����B���̏o�͂��ulog.csv�v�Ƃ����t�@�C���ɂ���B�v���O���������umm1k.sh�v�Ƃ���ƁA�g�p��́A
sh mm1k.sh 1 59 60 5 >log.csv
�Ƃ����悤�ɂȂ�B�V�F���X�N���v�g�ɂ��v���O�������ȉ��Ɏ����B
mm1k.sh
count=$1
while [ $count -le $2 ];
do
usr/bin/ns mm1k.tcl ${count}.0 ${3}.0 $4
perl mm1k.pl $count $3
count=`expr $count + 1`
done
�@�A�[����B�̗��_�l��![]() �A�A�[����C���̗��_�l��
�A�A�[����C���̗��_�l��
![]() �Ōv�Z���āAMicrosoft Office Excel 2003�Ő}�W�̂悤�ɂ����B����Ǝ����l���O���t�ɂ���ƁA�}�X�A�}�P�O�̂悤�ɂȂ����B
�Ōv�Z���āAMicrosoft Office Excel 2003�Ő}�W�̂悤�ɂ����B����Ǝ����l���O���t�ɂ���ƁA�}�X�A�}�P�O�̂悤�ɂȂ����B
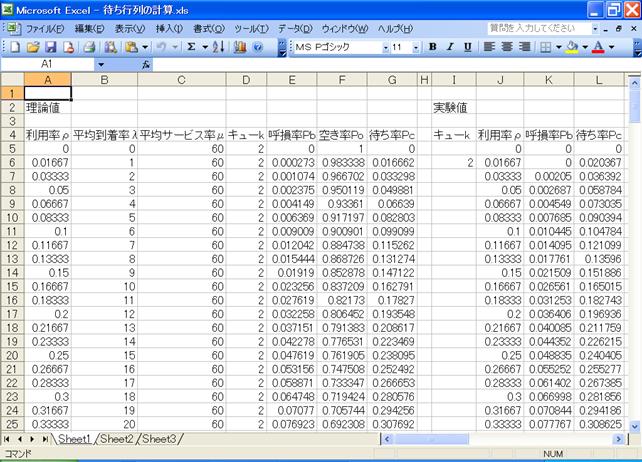
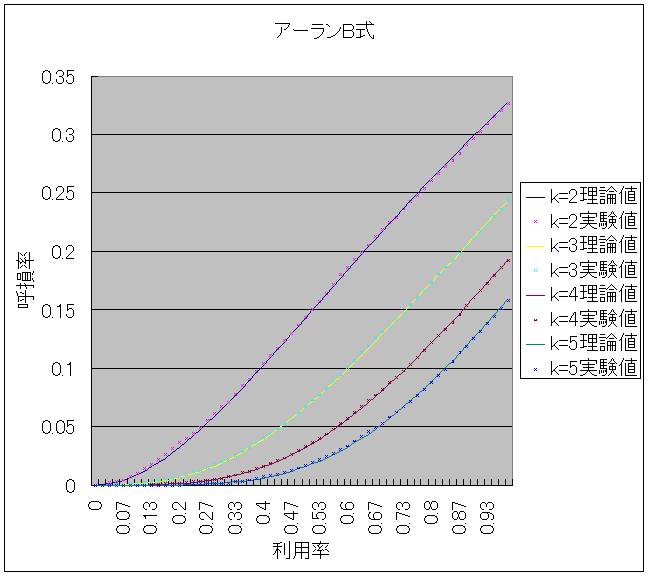
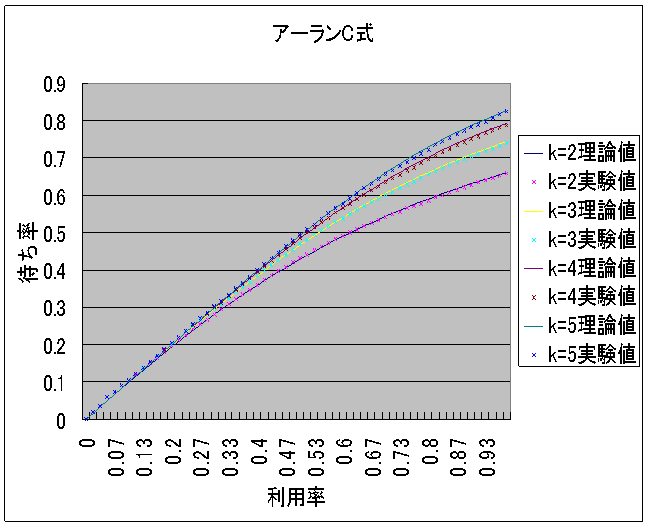
�@�A�[����B���̃O���t�́A�����l�Ɨ��_�l�͂قړ������B�A�[����C���̃O���t�́A���p�����オ��ɂ�Č덷��������������̂́A�ł��덷���傫���ꏊ�ł��덷���͖�O�D�T���Ȃ̂Ŏ����l�Ɨ��_�l�͂قړ������ƌ�����B
�@�҂��s�_�ɂ����Čđ����E�҂����̌v�Z�́A�������G�œ���Ȃ��̂������B�������ANS2��p�����V�~�����[�V�����v���O���������A���̃V�~�����[�V�������ʂ���͂��邱�Ƃɂ��A�đ����E�҂�����e�Ղɓ����邱�Ƃ��킩�����B�܂��A���̎�@�����p����A���[�^�̌đ����E�҂����̉�͂��\�ł���A���p���͂���B
�@���́A�҂��s�f���ő����������̂��̂̉�͂ɒ��킵�����B
mm1k.tcl
set lambda [lindex $argv 0]
set mu [lindex $argv 1]
set qsize [lindex $argv 2]
set ns [new Simulator]
set tf [open out.tr w]
$ns trace-all $tf
set n1 [$ns node]
set n2 [$ns node]
set link [$ns simplex-link $n1 $n2 100kb 0ms DropTail]
$ns queue-limit $n1 $n2 $qsize
set InterArrivalTime [new RandomVariable/Exponential]
$InterArrivalTime set avg_ [expr 1/$lambda]
set pktSize [new RandomVariable/Exponential]
$pktSize set avg_ [expr 100000.0/(8*$mu)]
set src [new Agent/UDP]
$ns attach-agent $n1 $src
set qmon [$ns monitor-queue $n1 $n2 [open qm.out w] 0.1]
$link queue-sample-timeout
proc finish {} {
global ns tf
$ns flush-trace
close $tf
exit 0
}
proc sendpacket {} {
global ns src InterArrivalTime pktSize
set time [$ns now]
$ns at [expr $time + [$InterArrivalTime value]] "sendpacket"
set bytes [expr round ([$pktSize value])]
$src send $bytes
}
set sink [new Agent/Null]
$ns attach-agent $n2 $sink
$ns connect $src $sink
$ns at 0.0001 "sendpacket"
$ns at 1000.0 "finish"
$ns run
mm1k.pl
open(IN, 'out.tr');
@temp = <IN>;
@plus;
@minus;
$receive=0;
$drop=0;
foreach $n1 (@temp){
chomp;
@d1 = split(/ /,$n1);
if($d1[0] eq '+'){
$plus[$d1[11]] = $d1[1];
}
elsif($d1[0] eq '-'){
$minus[$d1[11]] = $d1[1];
}
elsif($d1[0] eq 'r'){
$receive++;
}
elsif($d1[0] eq 'd'){
$drop++;
}
}
$i = 0;
$nowait = 0;
for ($i=0;$i<=$#minus;$i++){
if (defined($minus[$i])){
if ($minus[$i] == $plus[$i]){
$nowait++;
}
}
}
$koson=$dr/($dr+$re);
$mati=($drop+$receive-$nowait)/($drop+$receive);
$ro=$ARGV[0]/$ARGV[1];
print "$ro,$koson,$mati\n";
mm1k.sh
count=$1
while [ $count -le $2 ];
do
usr/bin/ns mm1k.tcl ${count}.0 ${3}.0 $4
perl mm1k.pl $count $3
count=`expr $count + 1`
done